Considere a quádrica dada por
(a) Determine a equação reduzida (sem termos mistos, nem lineares quando possível) e identifique a quádrica.
(b) Esboce o gráfico da quádrica identificando a origem e os eixos.
Passo 1
Sabemos que as quádricas no são definidas por equações do tipo:
![]()
Podem ser escritas na forma matricial fazendo:
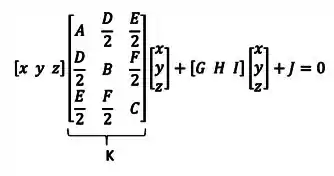
Nesse problema, temos a seguinte quádrica:
Vamos identificar os coeficientes:
Então a forma matricial vai ser:
Passo 2
Agora vamos precisar diagonalizar a matriz K dada por:
Vamos começar calculando os autovalores. O polinômio característico é:
Os autovalores são as raízes do polinômio característico, ou seja:
Logo, os autovalores são:
Agora vamos calcular os autovetores associado a cada autovalor.
Para :
Os autovetores são então as soluções do sistema:
Temos que:
E pela terceira equação:
Então as soluções são da forma:
E o autoespaço de é gerado por (1,1,0). Normalizando:
Para :
Os autovetores são então as soluções do sistema:
Temos que:
E pela terceira equação:
Então as soluções são da forma:
E o autoespaço de é gerado por (-1,1,0). Normalizando:
Tá acabando, falta só mais um!
Para :
Os autovetores são então as soluções do sistema:
Das duas primeiras equações, tiramos que:
Então as soluções são da forma:
E o autoespaço de é gerado por (0,0,1). Ele já está normalizado! Então:
Passo 3
Agora encontramos a base ortonormal de vetores:
Vamos escrevê-los nas colunas de uma matriz N:
A matriz de autovalores correspondente é:
Então, fazendo uma mudança de variáveis e denotando as novas variáveis por e , vamos ter que a forma matricial da quádrica vai ficar:
Completando quadrados:
Agora fazemos outra mudança de variáveis:
E aí vamos ter a quádrica:
Multiplicando os dois lados por -1:
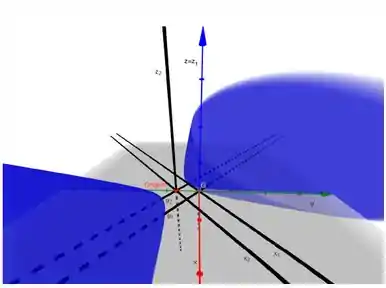
Como a equação tem 2 sinais negativos do lado esquerdo, ela representa um hiperboloide de duas folhas!
Passo 4
Depois de termos feito todo esse processo de passar para as variáveis e , obtemos um hiperboloide de duas folhas com origem em:
Como havíamos definido:
O ponto equivale a:
Na equação que obtemos, note que o sinal positivo está na variável
Então o hiperboloide vai se abrir ao longo do eixo .
O gráfico vai ficar assim:
Resposta
(a)
Hiperboloide de duas folhas
(b) Origem: