Uma lanterna está em repouso no sistema inercial que se move com velocidade em relação a um outro sistema inercial . Em um determinado instante, um pulso de luz é emitido pela lanterna e propaga-se paralelamente ao eixo até ser refletido por um espelho paralelo ao plano , retornando à lanterna. A distância entre a lanterna e o espelho é , conforme a figura.
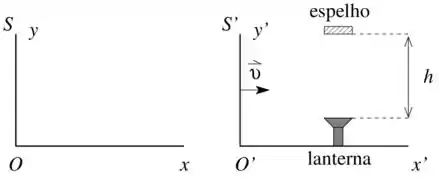
- Qual o intervalo de tempo medido em entre a emissão e o retorno do pulso luminoso?
- Qual a distância percorrida pela lanterna durante estes dois eventos (emissão e retorno do pulso), medida no referencial ?
Passo 1
Temos que o referencial é o referencial em repouso à lanterna, assim o tempo medido nesse referencial será o tempo próprio. Como a distância percorrida pela luz é e a velocidade da luz é , temos
Passo 2
Já sabemos a velocidade da lanterna em relação ao referencial (). Para obter a distância percorrida pela lanterna no referencial basta multiplicar essa velocidade pelo intervalo de tempo entre a emissão e retorno do pulso medido pelo referencial .
O pulo do gato agora é ver que, como o referencial não está em repouso em relação à lanterna, que o intervalo de tempo medido neste referencial será dilatado e se relaciona com o tempo próprio (do referencial ) por
Repare que (como tinha que ser)
Passo 3
Agora já estamos na cara do gol! A distância percorrida pela lanterna no referencial será