Exercícios de Relatividade do Tempo - Lista de Exercícios Resolvida

Um astronauta parte da Terra e viaja com velocidade de em direção à estrela Vega, que está a de distância. Quanto tempo terá passado, de acordo com os relógios da Terra, quando o astronauta chegar a Vega; quando os observadores terrestres receberem a notícia de que o astronauta chegou a Vega? Qual é a diferença entre o tempo de viagem de acordo com os relógios da Terra e o tempo de viagem de acordo com o relógio de bordo?

O píon negativo é uma partícula instável que possui vida média aproximadamente igual a (medida no sistema de referência do píon).

1. Quando o píon se desloca com velocidade muito grande em relação ao laboratório, sua vida média em relação ao laboratório é de . Calcule a velocidade do píon expressa como uma fração de .
2. Qual é a distância que o píon percorre no laboratório durante sua vida média?

Um píon é criado na parte superior da atmosfera da Terra quando um raio cósmico colide com um núcleo atômico. O píon assim formado desce em direção à superfície da Terra com uma velocidade de .

Em um referencial no qual estão em repouso os píons decaem com uma vida média de . No referencial da Terra, que distância um píon percorre (em média) na atmosfera antes de decair?

Os tripulantes da USS Enterprise NCC-1701, que se encontra a uma distância de da Terra, enviam uma mensagem para o centro de controle da Terra, avisando que irão cessar as comunicações durante , intervalo de tempo durante o qual o software da nave será atualizado.

Supondo que a Enterprise viaja a uma velocidade de em relação à Terra, quantos dias terão transcorrido na Terra nesse período?

12. Nenhuma das anteriores

Uma espaçonave se afasta da Terra com velocidade de em relação à Terra e a seguir volta com a mesma velocidade.

A espaçonave transporta um relógio atômico que foi cuidadosamente sincronizado com outro relógio que permaneceu na Terra.

A espaçonave retorna a seu ponto de partida dias (um ano) mais tarde, conforme medido pelo relógio que ficou na Terra.

Qual a diferença entre os intervalos de tempo, em horas, medidos pelos dois relógios?

Qual dos dois relógios, o que ficou na Terra ou o da espaçonave, indica o menor intervalo de tempo?

Uma partícula instável de alta energia entra em um detector e deixa um rastro com de comprimento viajando a uma velocidade de , antes de decair.

Qual é o tempo de vida próprio da partícula? Em outras palavras, quanto tempo a partícula levaria para decair se estivesse em repouso em relação ao detector?

Em uma primeira aproximação, determina-se que uma pessoa consiga viver em segurança dentro de uma nave espacial por anos (em relação à nave). Assumindo que a velocidade da nave é para um dado referencial inercial, calcule o tempo máximo que uma nave pode viajar, em relação ao referencial inercial, com o passageiro em segurança.

a) anos.

b) anos.

c) anos.

d) anos.

e) anos.

A partir dos princípios da Relatividade Restrita obtenha a relação entre o tempo próprio medido por um observador que se move com velocidade relativística em relação a outro referencial e o intervalo de tempo medido pelo observador no outro referencial (dito estacionário).

Um astronauta parte da Terra e viaja com velocidade de em direção à estrela Vega, que está a 26 anos-luz de distância da Terra. Quanto tempo terá decorrido de acordo com o relógio do astronauta ao chegar a Vega?

1. 54,2 anos
2. 34,7 anos.
3. 43,3 anos.
4. 26,0 anos.
5. Não há dados suficientes para se estimar o tempo.

Qual é a razão entre o tempo próprio e o tempo de vida de uma partícula instável em relação a um referencial inercial para o qual a partícula se desloca em movimento retilíneo e uniforme com da velocidade da luz?

Uma lanterna está em repouso no sistema inercial que se move com velocidade em relação a um outro sistema inercial . Em um determinado instante, um pulso de luz é emitido pela lanterna e propaga-se paralelamente ao eixo até ser refletido por um espelho paralelo ao plano , retornando à lanterna. A distância entre a lanterna e o espelho é , conforme a figura.

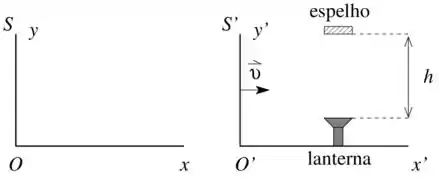
1. Qual o intervalo de tempo medido em entre a emissão e o retorno do pulso luminoso?
2. Qual a distância percorrida pela lanterna durante estes dois eventos (emissão e retorno do pulso), medida no referencial ?

Uma pessoa dentro de uma nave espacial observa uma bolinha bater no chão, ser ricocheteada no teto e voltar para a mesma posição inicial no chão. Um astronauta fora da nave observa o movimento da bolinha.

O tempo marcado pelo astronauta para o movimento total da bolinha é e a velocidade da nave em relação ao astronauta é .

Determine o tempo marcado pela pessoa dentro da nave para o movimento total da bolinha.

Uma partícula elementar produzida em um experimento de laboratório percorre 0,230 mm no interior do laboratório, com uma velocidade relativa ao laboratório de 0,960 c, antes de decair em outra partícula.

(a ) Encontre o tempo de vida próprio da partícula.

A distância entre duas cidades A e B é 180km, segundo indicam as marcas da estrada. Considere agora dois relógios. Um relógio carregado por um ciclista relativístico viajando com velocidade e um relógio de posse de um observador em repouso na Terra. Em quanto tempo o ciclista percorrerá o percurso A-B segundo:

(a) O relógio da Terra?

(b) O relógio do ciclista?

Expresse a resposta dos itens (a) e (b) em segundos.

Os tripulantes da USS Enterprise NCC-1701, que se encontra a uma distância de da Terra, enviam uma mensagem para o centro de controle da Terra, avisando que irão cessar as comunicações durante , intervalo de tempo durante o qual o software da nave será atualizado.

Supondo que a Enterprise viaja a uma velocidade de em relação à Terra, quantos dias terão transcorrido na Terra nesse período?

12. Nenhuma das anteriores

Thamyres e Tamara, famosa dupla sertaneja, são gêmeas idênticas.

Elas embarcam em suas naves espaciais individuais para um passeio pela Via Láctea e decolam simultaneamente. Thamyres tem a nave mais rápida.

Ambas retornam para a Terra simultaneamente.

Qual das seguintes afirmativas é verdadeira?

1. Thamyres está mais velha somente se ela viajou na mesma direção que Tamara.
2. Thamyres está mais velha somente se ela viajou na direção oposta a Tamara.
3. Tamara está mais velha somente se ela viajou na mesma direção que Thamyres.
4. Tamara está mais velha somente se ela viajou na direção oposta a Thamyres.
5. Tamara está mais velha.
6. Todas as afirmativas são falsas.

Uma partícula instável surge em uma determinada posição, move-se com velocidade constante de módulo e se desintegra após o intervalo de tempo de (decaindo em outras partículas), em relação ao referencial do laboratório. Determine o tempo de vida da partícula para o referencial inercial da partícula.

a) .

b) .

c) .

d) .

A partir dos princípios da Relatividade Restrita obtenha a relação entre o tempo próprio medido por um observador que se move com velocidade relativística em relação a outro referencial e o intervalo de tempo medido pelo observador no outro referencial (dito estacionário).

Considere um relógio que possui velocidade para um referencial inercial e que, em um dado instante, é inicializado quando passa pela origem desse referencial inercial. Ao percorrer a distância de a partir da origem do referencial inercial, determine o tempo cronometrado pelo relógio.

a) segundos.

b) segundos.

c) segundos.

d) segundos.

e) segundos.