Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema dos Eixos Paralelos

Ver Teoria
Exercício 8123456791011121314151617181920212223242526272829

Enunciado

Um objeto quadrado de massa m é formado de quatro varetas finais idênticas, todas de comprimento L e massa M , amarradas juntas. O objeto é fixado a uma barra, podendo girar em torno dela com velocidade angular ω , como mostrado na figura. O momento de inércia do objeto em relação ao eixo de rotação na figura é:

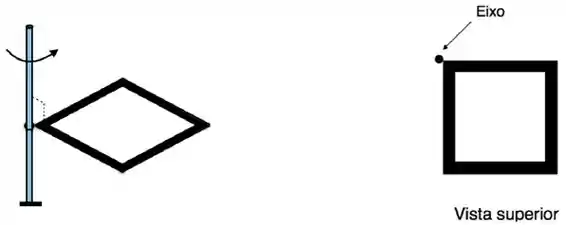
Passo 1

Bom, a gente tem que usar o que a gente sabe, né? Vamos usar aqui o teorema dos eixos paralelos. Da pra fazer de um modo direto, mas eu vou fazer em 2 passos porque eu acho que facilita as contas, fechou ?

Vamos primeiro calcular o momento de inercia em relação ao centro do quadrado, pode ser?

Passo 2

Cada barra em relação ao centro de massa do quadrado tem o seguinte momento de inércia:

I = I 0 + m d 2

Sendo:

I 0 = m l 2 12

m d 2 = m l 2 2 = m l 2 4

Como temos 4 barras, ficamos com o seguinte:

I c m = 4 I

I c m = 4 m l 2 12 + m l 2 4

I c m = 4 3 m l 2

Passo 3

Agora precisamos calcular em relação ao eixo dado, vamos usar teorema dos eixos paralelos novamente.

d = l 2   2

I e i x o = I c m + M d 2

I e i x o = 4 3 m l 2 + 4 m l 2   2 2

I e i x o = 4 3 m l 2 + 4 m l 2 2

I e i x o = 10 3 m l 2

Acho que não ia ter a resposta? Hahahaha, tem a resposta sim, só que ela usa a massa total das barras, que é M

4 m = M

I e i x o = 5 6 M l 2

Resposta

l e t r a   c )

Exercícios de Livros Relacionados

Calcule o momento de inércia de um aro (um anel fino) de raio R e massa M em relação a um eixo perpendicular ao plano do aro passando pela sua periferia.
Um disco uniforme de raio r e massa M gira em torno de um eixo horizontal paralelo ao seu eixo de simetria e que passa por um ponto de seu perímetro, de forma a poder oscilar livremente em um plano ve
Usando o teorema dos eixos paralelos e informações da Tabela 9.2, ache o momento de inércia da barra delgada de massa M e comprimento L indicado na Figura 9.23 em relação a um eixo passando pelo ponto
Uma barra delgada de comprimento L possui massa por unidade de comprimento variando a partir da extremidade esquerda, onde x = 0 , de acordo com d m / d x = γ x , onde γ é constante com unidades de k
Use a Equação (9.20) para calcular o momento de inércia de um disco maciço, uniforme, de raio R e massa M em relação a um eixo perpendicular ao plano do disco passando pelo seu centro.