Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema dos Eixos Paralelos

Ver Teoria
Exercício 5123467891011121314151617181920212223242526272829

Enunciado

UnB, Física I, Lista 11, questão 8

Uma placa metálica fina de massa M tem forma retangular com lados a e b . Use o teorema dos elementos paralelos para determinar seu momento de inércia em relação a um eixo perpendicular ao plano da placa passando por um dos seus vértices.

Passo 1

Oláaaaaa, galeraaaaa! Nessa questão precisamos encontrar o centro de massa e a distância do centro de massa até o eixo perpendicular. Assim podemos aplicar o teorema dos eixos paralelos. Para entender melhor vamos fazer um esboço disso, belê?

Passo 2

Temos um retângulo de lados a e b . Observe o esboço da figura. O centro de massa dessa placa fica exatamente no centro da figura e é representado por c m . Observe o ponto P , que foi escolhido para colocar o eixo perpendicular. Observe que a / 2 corresponde à metade do lado a e b / 2 correspondente à metade b .

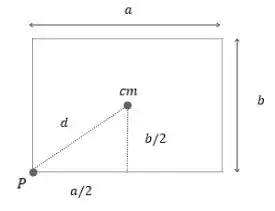
Passo 3

Observe que formamos um triângulo retângulo. Podemos utilizar o teorema de Pitágoras. Veja só:

d 2 = a 2 2 + b 2 2

Passando a raiz quadrada nos dois lados da equação, temos

d = a 2 2 + b 2 2

Além disso, por tabela, temos que o momento de inércia é

I c m = M 12 ( a 2 + b 2 )

Passo 4

Agora é possível aplicar o teorema dos eixos paralelos, que será:

I = I c m + M d 2                           ( I )

Temos que

d 2 = a 2 2 + b 2 2 = M 4 ( a 2 + b 2 )

Então, substituindo em ( I ) :

I = M 12 a 2 + b 2 + M 4 ( a 2 + b 2 )

Podemos simplificar a expressão, utilizando mínimo múltiplo comum. Veja só:

I = M + 3 M 12 a 2 + b 2

Por fim, a expressão fica

I = 4 M 12 a 2 + b 2

I = M 3 ( a 2 + b 2 )

Prontinho! Finalizamos!

Resposta

I = M 3 ( a 2 + b 2 )

Exercícios de Livros Relacionados

Calcule o momento de inércia de um aro (um anel fino) de raio R e massa M em relação a um eixo perpendicular ao plano do aro passando pela sua periferia.
Um disco uniforme de raio r e massa M gira em torno de um eixo horizontal paralelo ao seu eixo de simetria e que passa por um ponto de seu perímetro, de forma a poder oscilar livremente em um plano ve
Usando o teorema dos eixos paralelos e informações da Tabela 9.2, ache o momento de inércia da barra delgada de massa M e comprimento L indicado na Figura 9.23 em relação a um eixo passando pelo ponto
Uma barra delgada de comprimento L possui massa por unidade de comprimento variando a partir da extremidade esquerda, onde x = 0 , de acordo com d m / d x = γ x , onde γ é constante com unidades de k
Use a Equação (9.20) para calcular o momento de inércia de um disco maciço, uniforme, de raio R e massa M em relação a um eixo perpendicular ao plano do disco passando pelo seu centro.