Seja um subespaço de e . Sejam e as projeções de em e , respectivamente:
é verdadeira, mas é falsa
e são verdadeiras
e são falsas
é falsa, mas é verdadeira
Passo 1
Afirmativa :
Opa, lembra de quando aprendemos a calcular a matriz projeção usando mínimos quadrados? E eu mostrei esse desenho pra vocês:
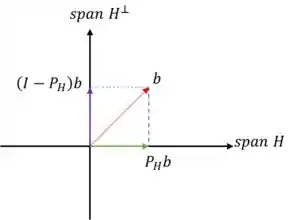
Pois então, repare que nele não estão definidas as dimensões de e ! Então na real ele vale para qualquer espaço, não só o que está desenhado haha. Então temos que a soma das projeções de um vetor em e dará sempre o próprio vetor! Logo, essa é verdadeira.
Passo 2
Afirmativa :
Pra essa podemos lembrar de Pitágoras! Sabemos que a equivalência correta seria:
Maaas, se você não tiver essa sacada geométrica de que a projeção sobre um espaço e seu complemento ortogonal forma um triângulo retângulo, pode resolver algebricamente também! Se liga:
O módulo da projeção de um vetor sobre um espaço é dado por:
Onde é o ângulo entre o vetor e nosso espaço . Nesse caso qual seria o módulo da projeção de sobre ? Bom, como é ortogonal a o ângulo entre eles é de . Se o ângulo entre e é de , então o àngulo entre e tem que ser , logo:
A afirmativa diz que:
Assumindo que temos:
O que não é verdade, logo essa é falsa.
Resposta
Letra