A3 T2 T12 T15
Sejam e vetores do e o ângulo entre eles:
- Se , então é ortogonal ao vetor
- Se os componentes de são todos menores que , em módulo, então
Ambas são verdadeiras.
Ambas são falsas.
é verdadeira e é falsa.
é falsa e é verdadeira.
Passo 1
Afirmativa :
Lembram que quando projetamos ortogonalmente o vetor o módulo da sua projeção é dado por:
Logo, o que essa afirmativa ta falando é que é a projeção de sobre algum subespaço que faz um ângulo com . Agora se liga nessa imagem:
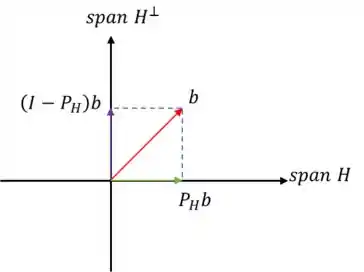
Nesse caso seria nosso vetor e seria nosso . Nesse caso podemos ver que é a projeção de sobre , que naturalmente vai ser ortogonal a já que ele é a projeção sobre . Então essa afirmativa é verdadeira.
Passo 2
Afirmativa :
Essa eu vou te provar que é falsa. Pega sendo:
Pronto, deu maior que !
Resposta
Letra
Exercícios de Livros Relacionados
1. Calcular o centróide dos vetores e representar geometricamente: u 1 = 1,2 e u 2 = 2,1 ; u 1 = 1,1 , u 2 = 1,2 , u 3 = 4 , - 1 e u 4 = 2,2 ; u 1 = 1,2 , 1 , u 2 = - 1 , - 2,0 e u 3 = 0,0 , - 1 ; u 1
3. Enunciar rigorosamente e provar: um operador linear do R n preserva os centróides.
4. Tomemos três vetores no R 2 , cujas extremidades formem um triângulo. Qual é o ponto do triângulo que coincide com a extremidade do centróide dos três vetores?
2. Seja u o centróide dos vetores u 1 , u 2 , … , u p do R n . Calcular nos exemplos do exercício 1 a soma u - u 1 2 + … + u - u p 2 .
Qual é a série de Fourier de s e n (3 x) ?