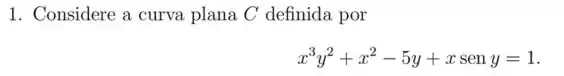
![]()
![]()
Passo 1
Aplicamos a derivada implícita nessa igualdade aí, com o cuidado de usar a Regra do Produto no primeiro termo e no termo do seno:
Passo 2
Agora vamos colocar o em evidência:
Passo 3
Sabemos que o coeficiente angular de uma reta modelada por valerá a derivada da função no ponto de tangência em que :
Logo, se , achamos :
Assim, a reta será