Ache a superfície de ponto , cuja distância ao eixo é 2/3 da distância de ao plano . Identifique a superfície.
Passo 1
O problema não fala diretamente em quádricas nessa questão. Bom, primeiramente vamos ilustrar geometricamente o que o problema nos informou. Chamando de a distância de ao eixo temos:
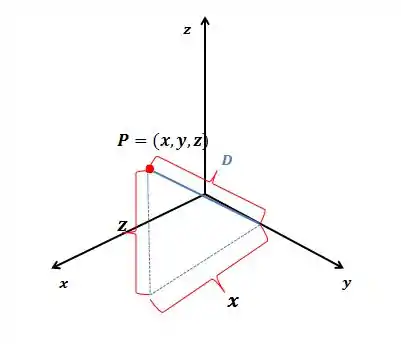
Passo 2
Agora, podemos encontrar uma equação para . Temos :
Passo 3
A distância de um ponto ao plano é a própria coordenada do ponto.
O problema diz que a distância ao eixo é 2/3 da distância ao plano . Então temos:
Que é a equação do cone circular.
Resposta
Cone circular com equação: