UFRJ, Cálculo 2, P1 2013.1, questão discursiva 2a
Considere a superfície definida por:
- Faça um desenho da superfície, destacando as curvas de interseção com os planos
Passo 1
a) Perceba que é um paraboloide elíptico, pois podemos escrevê-lo da forma:
Ajeitando:
Passo 2
Agora, vamos fazer os traços do paraboloide elíptico. Temos:
- , que é a circunferência no plano com centro em e raio
- , que é uma parábola no plano , com vértice em
- , que é uma parábola no plano , com vértice em
Passo 3
Juntando todas essas informações, vamos ter o seguinte esboço:
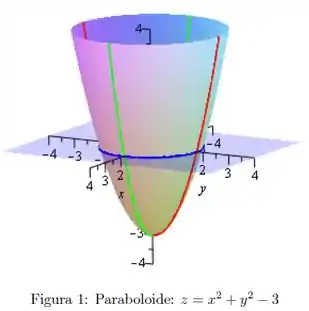
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Os Exercícios 45-48 fornecem equações para parábolas e nos dize quantas unidades para cima ou para baixo e para direita ou para esquerda cada parábola deve ser deslocada. Encontre uma equação para a n
Os Exercícios 45-48 fornecem equações para parábolas e nos dize quantas unidades para cima ou para baixo e para direita ou para esquerda cada parábola deve ser deslocada. Encontre uma equação para a n
Os Exercícios 45-48 fornecem equações para parábolas e nos dize quantas unidades para cima ou para baixo e para direita ou para esquerda cada parábola deve ser deslocada. Encontre uma equação para a n
A parábola y2 = 8x é deslocada 2 unidades para baixo e 1 unidade para a direita para gerar a parábola (y + 2)2 = 8(x - 1). a. Encontre o vértice, foco e diretriz da nova parábola.b. Represente grafica
A parábola X2 = -4y é deslocada 1 unidades para esquerda e 3 unidade para cima para gerar a parábola (x+1)=4(y-3) a. Encontre o vértice, foco e diretriz da nova parábola.b. Represente graficamente os