Identifique as superfícies quadráticas abaixo e esboce seu gráfico.
Passo 1
Antes de tentar identificar a Quádrica devemos completar os quadrados na equação, vamos começar pela marotamente porque não precisa completar o quadrado. Porque não precisa? Ele só tem caras ao quadrado ou sem estar elevado a ninguém. Se tivesse alguém ao quadrado e essa mesma letra não elevada ao quadrado ai sim iríamos completar quadrados.
Temos
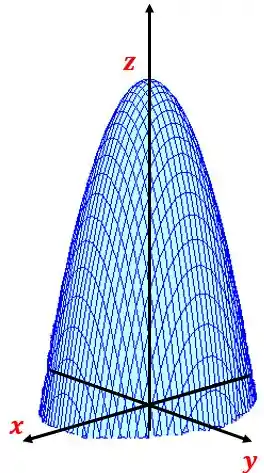
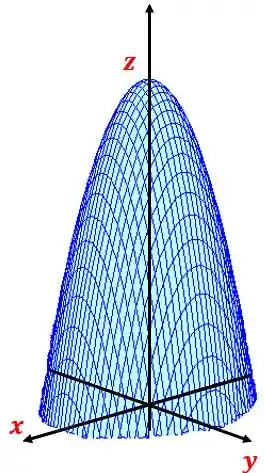
Como temos sem estar ao quadrado e e tem o mesmo sinal temos um paraboloide elíptico. Mas como não temos o sozinho ele está deslocado, fica atento a isso.
Ele vai ter a “Pontinha” no ponto
O gráfico vai ficar
Passo 2
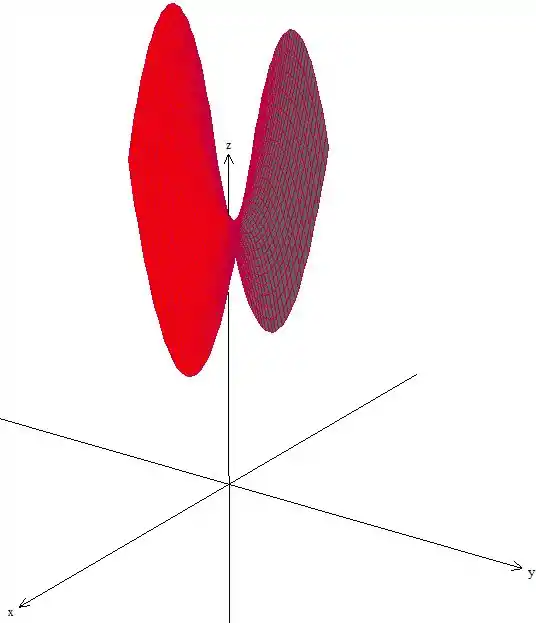
A superfície também não precisa completar quadrado, fica muito atento que agora temos uma equação onde os sinais dos caras ao quadrado são diferente, isso nos diz que isso é um paraboloide hiperbólico, vulgo sela.
O gráfico vai ficar
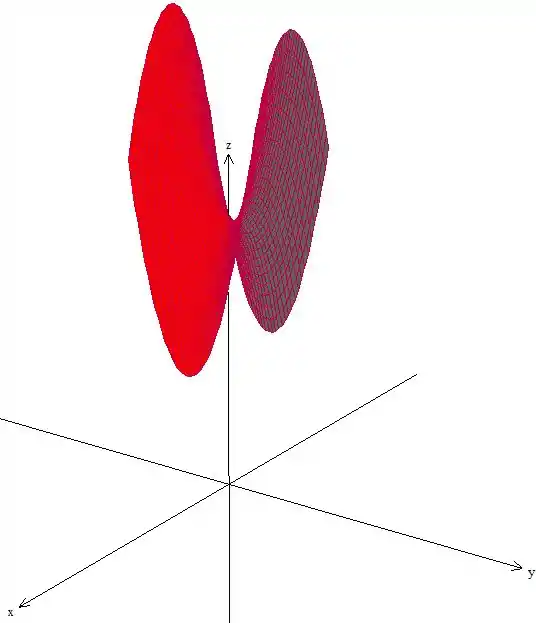
Repara que o eixo da sela está na direção do eixo , só que deslocado para cima, ou seja, com , que é o que aquele está fazendo.
Resposta