O diagrama abaixo descreve processos diferentes entre dois estados inicial e final, respectivamente e , sofridos por 1 mol de um gás ideal. Considere como sendo .
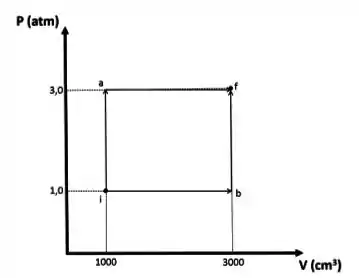
Calcule as temperaturas deste gás nos estados inicial e final , a saber os pontos e , respectivamente, no diagrama abaixo.
e
e
e
e
e .
e .
Passo 1
Vamos usar a equação geral dos gases para descobrir a temperatura inicial, visto que temos pressão, volume, dados no gráfico, e número de mols dado no enunciado.
Isolando a temperatura temos que
Assim para descobrirmos a temperatura inicial, basta substituirmos os dados do estão inicial
Faremos o mesmo para achar a temperatura do estado final:
Por isso a alternativa correta é a
Resposta
Alternativa
Exercícios de Livros Relacionados
60. Um frasco com volume de 1,50L , equipado com uma válvula, contém o gás etano ( C 2 H 6 ) a 300K e à pressão atmosférica ( 1,03 ⋅ 10 5P a ) . A massa molar do etanol é 30,1g / m o l . O sistema é a
Determine a massa em quilogramas de 7,50.10 24 átomos de arsênio, que tem uma massa molar de 74,9g / m o l .
Um pneu de automóvel tem um volume de 1,64.10 - 2m 3 e contém ar à pressão manométrica (pressão acima da pressão atmosférica) de 165k P a quando a temperatura é 0,00° C . Qual é a pressão manométrica
Uma amostra de oxigênio com um volume de 1000c m 3 a 40,0° C e 1,01.10 5P a se expande até um volume de 1500c m 3 a uma pressão de 1,06.10 5P a . Determine (a) o número de mols de oxigênio presentes n
Você copia o seguinte parágrafo de um livro de física marciano: "1 snorf de um gás ideal ocupa um volume de 1,35 Zaks. A uma temperatura de 22 glips, o gás tem uma pressão de 12,5 klads. A uma tempera