Banco de Questões - Estácio de Cálculo Diferencial e Integral II da UNESA - AV2
Cálculo Diferencial e Integral II - UNESA
Calcule a velocidade da curva , indicando a única resposta correta. Considere a resposta em .
(a)
(b)
(c)
(d)
(e)
Ver solução completaSabendo que o comprimento de onda de uma curva lisa , é dada pela fórmula:
Encontre o comprimento da curva , .
Ver solução completaEncontre a área da região limitada pela parábola e pela reta utilizando integral dupla.
(a)
(b)
(c)
(d)
(e)
Ver solução completaSeja . Calcular o valor da integral tripla da função em relação às variáveis e onde varia no intervalo , varia no intervalo e varia no intervalo .
(a)
(b)
(c)
(d)
(e)
Ver solução completaConsidere a função .
Identifique as afirmações verdadeiras (V) e as falsas (F):
( ) A derivada da função em na direção do vetor é nula.
( ) A função aumenta mais rapidamente na direção do vetor .
( ) Existe uma direção na qual a taxa de variação da função é .
( ) A taxa da variação da função é .
( ) A reta tangente à curva no ponto é .
- (1) V (2) V (3) V (4) V (5) F
- (1) F (2) V (3) V (4) V (5) F
- (1) V (2) V (3) F (4) V (5) V
- (1) V (2) V (3) F (4) V (5) F
- (1) V (2) V (3) V (4) F (5) F
Calcule a velocidade de uma partícula com vetor de posição . Indique a única resposta correta.
Resolva a equação diferencial para como função vetorial de :
Com a condição inicial: .
Ver solução completaCalcular em que é a hélice definida por , e o campo vetorial definido por .
(a)
(b)
(c)
(d)
(e)
Ver solução completaDuas aeronaves viajam pelo espaço com trajetórias diferentes dadas pelas funções vetoriais:
(a) As aeronaves não colidem.
(b) As aeronaves colidem no instante .
(c) As aeronaves colidem no instante .
(d) As aeronaves colidem no instante .
(e) As trajetórias não se interceptam.
Ver solução completaSendo encontre a soma das derivadas parciais da função em relação a cada variável no ponto .
O vetor de posição de um objeto se movendo em um plano é dado por .
Determine a velocidade do objeto no instante .
Ver solução completaSeja o vetor posição de uma partícula que se move ao longo de uma curva lista no plano.
Considere as afirmações. Assinale (V) ou (F):
- ( ) Quando uma partícula se move durante um intervalo de tempo , as coordenadas da partícula são . Os pontos formam uma curva que é a trajetória da partícula;
- ( ) A velocidade é a derivada da posição, isto é: ;
- ( ) O módulo da velocidade ou a magnitude da velocidade é igual a ;
- ( ) A aceleração é a derivada da velocidade, ou seja, ;
- ( ) O vetor unitário ou versor é a direção do movimento no instante ;
- ( ) é lisa se for contínua e nunca ;
- (1) V (2) F (3) F (4) V (5) F (6) V
- (1) V (2) F (3) V (4) V (5) V (6) V
- (1) V (2) V (3) V (4) V (5) V (6) F
- (1) V (2) V (3) F (4) V (5) V (6) F
- (1) V (2) F (3) V (4) V (5) V (6) F
Considere uma função de três variáveis que tem derivadas parciais contínuas , , em algum intervalo e e são funções de outra variável .
Então .
Diz-se que é a derivada total de em relação a e representa a taxa de variação de à medida que varia.
Supondo onde , , , calcule sendo .
Ver solução completaCalcule a integral:
Onde é o quadrado cortado no primeiro quadrante pelas retas e
Ver solução completaSeja a posição de uma partícula no plano no instante . Encontre o vetor velocidade e aceleração da partícula no instante .
Ver solução completaA integral fornece a área de uma região no plano . Esboce a região, identifique cada curva limite com sua equação, escreva as coordenadas dos pontos onde há intersecção das curvas. Depois encontre a área da região.
Ver solução completaA Lemniscata de Bernoulli é a curva algébrica do quarto grau de equação cartesiana:
A Lemniscata é a figura geométrica com a forma de uma hélice, similar ao numeral e ao símbolo de infinito . Pode ser descrita por coordenadas polares:
Calcular a área dentro da Lemniscata:
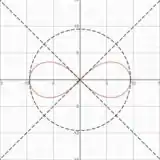
Sabendo que no primeiro quadrante deve-se considerar e .
Ver solução completaConverta a integral abaixo para uma integral equivalente em coordenadas cilíndricas e calcule o resultado.
Ver solução completaMude a integral cartesiana para uma integral polar equivalente e calcule a integral polar de:
Transforme para o sistema de coordenadas polares a integral
Em seguida, calcule o seu valor.
Considere a função .
Identifique as afirmações verdadeiras (V) e as falsas (F):
( ) A derivada da função em na direção do vetor é nula.
( ) A função aumenta mais rapidamente na direção do vetor .
( ) Existe uma direção na qual a taxa de variação da função é .
( ) A taxa da variação da função é .
( ) A reta tangente à curva no ponto é .
- (1) V (2) V (3) V (4) V (5) F
- (1) F (2) V (3) V (4) V (5) F
- (1) V (2) V (3) F (4) V (5) V
- (1) V (2) V (3) F (4) V (5) F
- (1) V (2) V (3) V (4) F (5) F
Considere uma distribuição de temperatura em uma região do espaço. Uma partícula localziada em precisa esquentar rapidamente. Outra partícula precisa resfriar-se o mais rápido possível. Qual é a taxa máxima de descrescimento da temperatura em .
Ver solução completaé a posição de uma partícula no espaço no instante . Encontre o ângulo entre os vetores aceleração e velocidade no instante para
Ver solução completaInverta a ordem da integral, esboce a região de integração se achar necessário e calcule a integral:
Ver solução completaSeja . Calcular o valor da integral tripla da função em relação às variáveis e onde varia no intervalo , varia no intervalo e varia no intervalo .
(a)
(b)
(c)
(d)
(e)
Ver solução completaUse o Teorema de Green para encontrar a circulação no sentido anti-horário e o fluxo exterior para o campo e a curva : quadrado limitado por , , , .
Ver solução completa