Uma bolinha homogênea de massa e raio rola sem deslizar sobre uma calha cilíndrica de raio , na vizinhança do fundo, ou seja, na aproximação de ângulos pequenos. Dado
- Faça um esquema das forças que agem sobre a bola e determina a força resultante.
- Escreva e .
- Mostre que o sistema é um oscilador com frequência angular .
- Mostre que a função , onde e são constantes é solução da equação diferencial.
- Considerando que no instante o ângulo é e a velocidade é , determine a solução particular para este oscilador em termos de , , , e .
- Escreva as expressões para e , sendo , a energia potencial e a energia cinética.
- Mostre que é independente do tempo.
Passo 1
a):
Esquema:
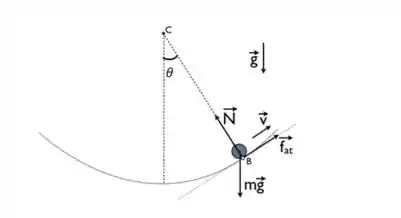
Vamos agora calcular o somatório das forças tangenciais e radiais.
Radiais:
A normal já está na direção radial, então não precisamos decompô-la. Já o peso e a força de atrito precisam ser decompostas em:
A força de atrito não tem uma componente na direção radial pois é sempre tangente a trajetória.
A a resultante das forças dá:
Só que a gente sabe da mecânica que:
Logo:
E as forças na direção tangencial:
Precisamos decompor novamente o peso. A força de atrito já está na direção tangencial e a força normal é perpendicular à trajetória, logo:
Logo, a resultante é:
Passo 2
b):
A energia potencial é dada por:
Bom, é a distância da bolinha até o chão. Vamos dar uma olhada no esquema:
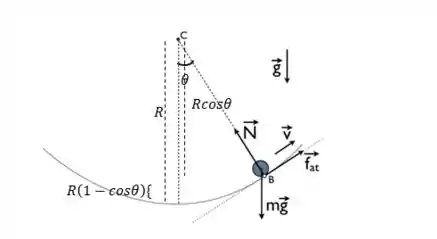
O nosso vai ser aquele pedacinho ali, que pode ser calculado como:
Logo, a energia pode ser calculada por:
Queremos saber também , ou seja, a energia cinética em função da velocidade angular.
A energia cinética terá uma contribuição devido à rotação da esfera em torno de seu centro de massa e uma contribuição devido a translação do centro de massa.
Sendo:
é um diferencial de pois esse ângulo é relativo à rotação da bolinha sobre o seu próprio eixo, e não o Ângulo maior na calha. Mas se não houver deslizamento:
Logo:
Logo:
Onde usamos .
Consideremos que :
Passo 3
c):
Vamos resolver essa usando o fato de que a energia mecânica se conserva.
A energia mecânica é:
Logo:
Logo:
Sendo:
E:
Vamos concluir a equação acima, lembrando de derivar corretamente, usando a regra da cadeia:
Ou seja, ou:
O que implicaria em , o que não é o caso. Ou:
Que é única possibilidade. Legal, mas isso é a equação de um oscilador! Para , temos :
Comparando com uma equação de MHS, vemos que :
Pronto (:.
Passo 4
d):
Vamos fazer as derivadas da função e substituir na equação diferencial pra provar:
Substituindo em :
Sendo :
Fica:
Como queríamos demonstrar!
Passo 5
e):
Bom, já sabemos o valor de . Basta a gente descobrir o valor de e agora.Considerando que no tempo a velocidade e o espaço inicial são e :
Logo:
Opa! Mas ali a gente escreveu e .Vamos escrever isso em função de e . Como podemos sempre escrever:
Que é definição de radiano. Podemos escrever em função do ângulo inicial e da velocidade angular inicial:
Logo:
E sendo:
A gente pode fazer umas manipulações e tirar o ângulo usando arco tangente:
Logo:
Então a equação ficará:
Passo 6
f):
Aqui a gente vai precisar usar uma aproximação para ângulos pequena aplicada ao cosseno:
A energia potencial fica:
Ai vem o pulo do gato. Sabemos uma função do tempo para
Vamos fazer algo parecido cm a energia cinética:
Sendo:
Sendo:
Passo 7
g):
Vamos somar as duas expressões que achamos e ver o que acontece:
Perfeito! As partes trigonométricas, que eram dependentes do tempo, se cancelaram pois .
Resposta
a):
esquema.
b):
c):
Demonstração
d):
Demonstração.
e):
f):
g):
Demonstração.