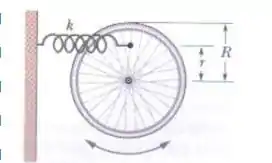
Uma roda pode girar livremente em torno do seu eixo fixo. Uma mola é presa a um dos raios a uma distância de do eixo, como mostra a figura. A roda gira em torno de seu centro.

(a) Supondo que a roda é um disco de massa e o raio , qual é a frequência angular das pequenas oscilações desse sistema em termos de e da constante elástica . Qual é o valor de para :

(b)

(c) ?

Dado:

Momento de inércia de um disco:

a) De cara, o enunciado tá pedindo a frequência angular. Então vamos tentar calcular isso!

Lembra da equação do MHS? Essa aqui:

Vamos tentar achar algo parecido com isso, que aí saberemos que o termo que acompanha o x é , sacou? Show! Mas como esse cara tá RODANDO (e não se deslocando linearmente) vamos ter que usar deslocamentos angulares, não lineares. Vamos usar então em vez de :

Agora vamos escrever a Lei de Newton para rotações (aquela que considera torque em vez de força):

Em que é o momento de inércia.

A única força que temos causando torque é a força da mola. Essa força será:

Porque, como são pequenas oscilações, a compressão da mola pode ser dada por , que é o arco do círculo no movimento. Já o torque, vai ser essa força vezes a distância até o centro:

Igualando isso ao torque resultante:

Dividindo todo mundo por :

Comparando com o MHS pra rotações:

Ok, agora podemos continuar.