Na Figura abaixo, uma placa de metal está montada em um eixo que passa pelo seu centro de massa. Uma mola com está ligada a uma parede e a um ponto da borda da placa a uma distância do centro de massa. Inicialmente a mola está relaxada. Se a placa é girada de 7° e liberada, oscila em torno do eixo em um MHS, com sua posição angular dada pela a outra figura. A escala do eixo horizontal é definida por . Qual é o momento de inércia da placa em relação ao centro de massa?
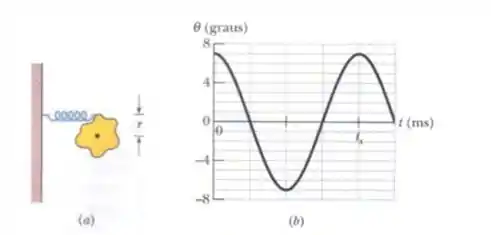
Passo 1
A força elástica produzirá um torque que vai ser dado por
Isso porque a força elástica é praticamente horizontal e o vetor posição que sai do centro da catraca até o ponto onde tá a mola é praticamente vertical.
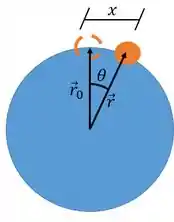
Já esse deslocamento em vai ser dado por
Para ângulos pequenos , assim
Como
Assim
Como
Passo 2
Bom, nós temos e dados pelo enunciado.
Temos
Na verdade, não diretamente, mas dê uma olhada no gráfico da variação angular: O ciclo se repete em , certo?
Então, esse tempo será o período:
Passo 3
Assim, poderemos achar