Exercícios de Probabilidade Conjunta de V.A. Bidimensionais Contínuas - Lista de Exercícios Resolvida
Questão 1
Seja um vetor bivariado de v.a.’s contínuas com a seguinte função:
Calcule o valor da constante para que seja uma função de densidade de probabilidade conjunta das variáveis aleatórias e .
Ver solução completaQuestão 2
Suponha e dois valores de probabilidade conhecidos. Assumindo duas v.a.’s discretas com distribuição conjunta para , e . Mostre como encontrar:
- O valor de , em função de e , para que seja uma distribuição conjunta. E escreva a função conjunta.
- A marginal de e de e indique qual o nome (modelo) destas distribuições.
- Podemos afirmar que e são independentes? Justifique sua resposta.
Questão 3
Sejam e v.a.’s contínuas com densidade conjunta:
- Encontre a constante que faz desta expressão uma densidade.
- Encontre a densidade marginal de e de
Questão 4
- Determine a constante para que seja uma função de probabilidade das variáveis aleatórias e .
- Encontre a densidade marginal de e de .
- Encontre a densidade condicional de dado .
- e são independentes? Por quê? Justifique.
Questão 5
Sejam e v.a. contínuas com densidade conjunta:
Dados:
Marginal de :
Marginal de :
Pede-se:
- Densidade condicional de dado .
- Média condicional de dado , e calcule o valor quando .
Questão 6
Sejam variáveis aleatórias contínuas com função densidade de probabilidade conjunta dada por
e caso contrário. A probabilidade vale:
Ver solução completaQuestão 7
Duas variáveis aleatórias contínuas têm densidade de probabilidade conjunta dada por:
caso contrário.
A densidade condicional de dado , para é?
Ver solução completaQuestão 8
Considere a seguinte densidade conjunta
- Ache a densidade marginal de .
- Ache a densidade marginal de .
- Calcule .
Questão 9
Se a função de probabilidade da variável aleatória contínua é dada por:
- Determine a constante para que seja uma função de probabilidade das variáveis aleatórias e , mostre a função ?
- Encontre a densidade marginal de e a densidade marginal de .
- Encontre a densidade condicional de dado .
Questão 10
- Determine a constante para que seja uma função de probabilidade das variáveis aleatórias e .
- Encontre a densidade marginal de e de .
- Encontre a densidade condicional de dado .
- e são independentes? Por quê? Justifique.
Questão 11
Sejam e v.a.’s contínuas com densidade conjunta:
- Encontre a constante que faz desta expressão uma densidade.
- Encontre a densidade marginal de e de
- Encontre a densidade condicional de dado .
Questão 12
Duas variáveis aleatórias independentes possuem as respectivas funções densidades de probabilidades marginais:
0, caso contrário;
0, caso contrário.
O valor deé:
Ver solução completaQuestão 13
Sejam e v.a.’s discretas com densidade conjunta:
Pede-se:
- Determine a constante para que seja uma função de probabilidade das variáveis aleatórias e , mostre a função ?
- Encontre a densidade marginal de e .
- e são independentes? Por que? Justifique.
Questão 14
Duas variáveis aleatórias têm densidade conjunta igual a para e igual a fora dessa região. O valor de é:
Ver solução completaQuestão 15
Admite-se que cada pneu dianteiro de um determinado tipo de veículo deve ter a pressão de 26 psi. Suponha que a pressão real em cada pneu seja uma variável aleatória para o pneu direito e para o pneu esquerdo, com a seguinte função de densidade conjunta:
Pede-se:
a) Qual é a probabilidade de os dois pneus estarem com pressão inferior ao ideal?
b) Determine a média condicional dado .
Ver solução completaQuestão 16
a) Suponha que e sejam variáveis aleatórias contínuas, prove que .
Observação: podemos dizer que é uma variável aleatória, que é uma função de .
b) Seja , , ..., uma sequência de variáveis aleatórias independentes com distribuição . Se , qual a distribuição de e de ?
Ver solução completaQuestão 17
Seja “” e “” duas Variáveis aleatórias discretas cuja função de probabilidade conjunta é expressa por:
a) Determine a constante “” para que seja uma função de probabilidade das variáveis aleatórias e .
b) Encontre a densidade condicional de dado .
Ver solução completaQuestão 18
Seja variável aleatória contínua com a seguinte função de densidade de probabilidade conjunta:
Pede-se:
- Calcular o Coeficiente de Correlação .
- Calcular a variância condicional de dado .
Questão 19
Seja um vetor bivariado de v.a.’s contínuas com a seguinte função:
Calcule o valor da constante para que seja uma função de densidade de probabilidade conjunta das variáveis aleatórias e .
Ver solução completaQuestão 20
Sejam e e v.a.’s contínuas com densidade conjunta expressa por:
Pede-se:
- Densidade marginal de e .
- e são independentes? Por que? Justifique.
Questão 21
Suponha e dois valores de probabilidade conhecidos. Assumindo duas v.a.’s discretas com função de probabilidade conjunta , para , e .
Pede-se:
- Calcular o valor da constante “ e apresentar a função de probabilidade conjunta em termos de e .
- A função de probabilidade condicional de dado .
Questão 22
- Determine a constante para que seja uma função de probabilidade das variáveis aleatórias e .
- Encontre a densidade marginal de e de .
- e são independentes? Por quê? Justifique.
Questão 23
Seja um vetor bivariado de v.a.’s contínuas com a seguinte função:
a) Calcule o valor da constante para que seja uma função de densidade de probabilidade conjunta das variáveis aleatórias e . Apresente a função conjunta.
b) Ache a média e a variância condicional de dado que .
c) e são independentes? Por quê? Justifique.
Ver solução completaQuestão 24
Suponha e dois valores de probabilidade conhecida. Assumindo duas v.a.’s discretas com distribuição conjunta , para e , mostre como encontrar:
a) O valor de em função de e , para que seja uma distribuição conjunta. Apresente a função conjunta somente em função de e .
b) A densidade condicional de dado
c) Podemos afirmar que e são independentes? Justifique sua resposta.
Ver solução completaQuestão 25
A função de densidade de probabilidade conjunta para duas variáveis aleatórias para uma constante é dada por:
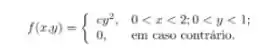
A densidade marginal de para
Ver solução completaQuestão 26
Obtenha , se a função de densidade de probabilidade conjunta das variáveis aleatórias é:
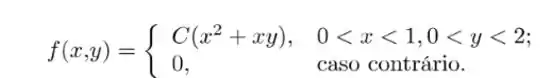
Questão 27
A função de densidade de probabilidade conjunta de duas variáveis aleatórias é dada por:
![]()
A densidade condicional de dado para é:
Ver solução completaQuestão 28
02) Dois números, e , são gerados aleatoriamente e uniformemente distribuídos no intervalo . Assuma que são gerados de maneira independente e calcule a probabilidade da equação possuir raízes reais.
a)
b)
c) .
d)
e)
Ver solução completaQuestão 29
Considere variáveis aleatórias com densidade conjunta constante na região e igual a zero no complemento dessa região. A densidade marginal de para é:
Ver solução completaQuestão 30
Dada a seguinte distribuição de probabilidades, calcular média da variável :
![]()
Questão 31
Considere a função de densidade conjunta para e caso contrário. Qual é a probabilidade de pertencer à região descrita por ? (Note: senecessário utilize as aproximações ; ; )
Ver solução completaQuestão 32
O valor da variável é um número no intervalo escolhido segundo uma densidade uniforme. De maneira similar, o valor da variável é um número no intervalo , escolhido segundo uma densidade uniforme. As variáveis são independentes. Um aluno toma os valores de obtidos em um experimento e desenha um triângulo retângulo, onde são os catetos. Qual a probabilidade que a hipotenusa desse triângulo seja menor que ?
Ver solução completa