Calcule
na região mostrada na figura abaixo,
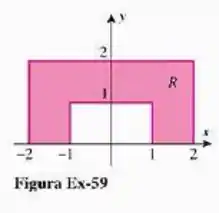
Passo 1
Bem, vamos começar escrevendo essa região, ok? Para isso, vamos dividí-la em partes:
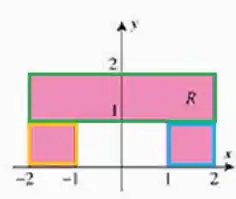
Chamando o retângulo verde de , o amarelo de e o azul de , temos o seguinte:
Passo 2
Agora, vamos encontrar os inter valos de cada integral.
Para o retângulo verde, temos:
Para o amarelo:
Para o azul:
Passo 3
Aplicando o Teorema de Fubini, temos:
Repare que a ordem dos intervalos está de acordo com a ordem dos diferenciais!
Passo 4
Agora, vamos resolver a integral de :
Passo 5
Calcular a integral de :
Passo 6
Calcular a integral de :
Passo 7
Somar os resultados encontrados