UFABC. Cálculo. Funções de Várias Variáveis. Lista 6 - Integrais Duplas. Questão 1a.
1 - Calcule , onde:
a) e é o retângulo ;
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nessa questão, vamos obter a integral dupla de em , onde é formado pelo retângulo .
Não entendeu nada? Relaxa, vamos devagar
é a região descrita por um retângulo que em varia entre e , e em varia entre e , formando assim
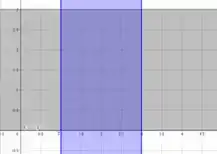
Nessa área temos que calcular o volume que forma, ou seja, a integral de limitada por esse retângulo.
E ai? Melhorou?
Bora lá
Passo 2
Primeiro vamos montar a integral. No enunciado foi dito que
Se , logo
Agora vamos substituir na nossa integral.
Aqui temos que colocar os limites que queremos integrar, por exemplo, queremos integras de a em então esse é nosso limite de integração em .
Já em , nosso limite de integração é de a .
Ok, mas como colocamos isso na integral?
Observe no fim da integral está escrito , ou seja, primeiro vamos integrar com relação a e depois com relação a .
Com isso, nos aplicamos os limites de integração da seguinte maneira
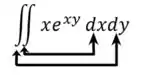
O símbolo de integração mais próximo de representa o primeiro na ordem de integração e o mais longe é o segundo.
Em cima vai o maior número pois nesse saco estamos integrando do maior para o menor.
Ou seja
Entendeu? 😎
Passo 3
Para facilitar nossos cálculos podemos inverter as integrais, veja só
Quando fazemos isso, temos que mudar de ordem e trocar as integrais.
Com isso, vamos calcular a integral com relação a
Assim como na derivada, a integral de é o próprio , então
Simplificando o resultado, temos
Tranquilo até aqui?
Passo 4
Agora vamos aplicar esse resultado na integral de .
Assim como em derivadas, a integral de uma soma é igual a soma das integrais, logo
Sabemos que a integral de é igual a e a integral de é igual a
Aplicando os limites de integração, temos
Com isso, chegamos no resultado de
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍