Uma casca cilíndrica é feita de um material condutor de condutividade uniforme. As dimensões do cilindro estão indicadas na figura, onde . As superfícies interna e externa da casca com raios e , onde é a distância até o eixo da casca cilíndrica, são duas equipotenciais mantidas a uma ddp igual a por uma bateria, conforme a figura.
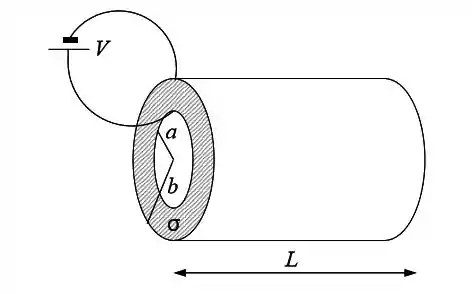
(a) Devido à simetria, a densidade de corrente é dada por . Calcule como função de , suposta conhecida.
(b) Calcule o vetor no interior da casca como função de .
(c) Calcule a resistência da casca.
(d) Calcule o ponto em função de e .
Passo 1
(a) A gente sabe que as cargas não são criadas e nem destruídas, portanto, podemos usar a conservação das cargas da seguinte maneira: A corrente através de qualquer superfície cilíndrica de raio dentro da casca é a mesma.
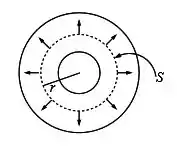
Como é a densidade de corrente elétrica:
Passo 2
(b) A lei de Ohm na forma vetorial nos diz que:
Portanto, temos que a densidade da corrente está na direção radial, então:
E então, usando o resultado obtido na letra (a):
Passo 3
(c) A diferença de potencial entre os raios e pode ser calculada da seguinte maneira:
Utilizando a resposta da letra (b), temos:
Lembrando que e que , obtemos
(d) Cálculo de J(a):
E aplicando o resultado da letra (c):
Resposta
a)
b)
c)
d)