UFSCAR, Sem Campus, Física 1, Listas Física 1 - UFSCAR - Lista 2 - Dinâmica, Questão 3
Um carro de massa está fazendo uma curva circular de raio , que possui inclinação com o chão. Seja o coeficiente de atrito cinético e a magnitude da aceleração da gravidade. Derive uma expressão para um intervalo de velocidade possível necessário para manter o carro movendo no círculo sem derrapar. Expresse suas respostas através das constantes mencionadas no exercício.
Passo 1
Eaew, tudo certinho contigo?
É um pouco complicado descrever a situação com palavras, a melhor opção é indicar um esquema, temos o seguinte
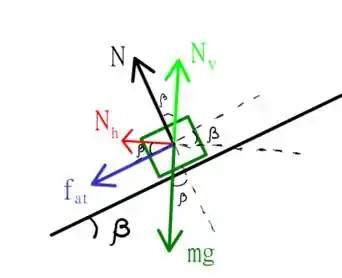
o quadrado verde acima representa o carro, o plano inclinado representa a nossa curva inclinada, e o carro se move entrando no papel. A situação colocada acima irá nos dar a velocidade máxima que o carro poderá ter sem que ele derrape para cima (efeito da tendência a sair da curva do carro), por isso a força de atrito aponta para baixo! Beleza? Também existirá uma velocidade mínima para o carro não derrapar para baixo da curva, isso inverterá a força de atrito, ou seja, teremos que
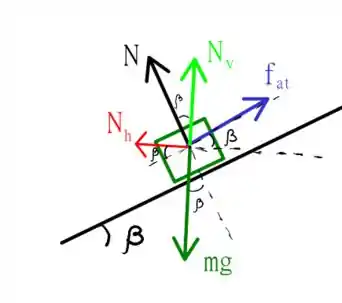
Agora será tudo uma questão de aplicar a segunda lei de Newton e obter nossas velocidades! Bora lá!
Passo 2
Vamos achar primeiro a velocidade máxima, para isso, usando a segunda lei de Newton teremos as seguintes equações
em que é a componente da força de atrito na horizontal, esse é o plano do movimento circular, por isso estamos considerando a aceleração centrípeta que possibilita a curva! Para o movimento vertical temos
Através das duas equações acima seremos capazes de obter a velocidade máxima! Vem comigo!
Passo 3
Vamos lembrar algumas definições! Primeiro, temos que aceleração centrípeta é tal que
em que é a velocidade que desejamos! Também temos que
em que é o coeficiente de atrito. Aqui temos um problema com o enunciado, ele nos indica como o coeficiente de atrito cinético, que é em geral menor do que o coeficiente de atrito estático, portanto, não é possível obter uma velocidade máxima (mínima) para o carro não derrapar. Vamos fazer o cálculo como deveria, mas mantenha em mente, que em geral, o carro poderia ir mais rápido ou mais devagar, mesmo sob as condições adequadas apresentadas acima! Vamos continuar a questão!
Passo 4
Usando o esquema apresentado acima, temos que
e
temos também que
Substituindo tudo na equação temos que
ou isolando a velocidade, temos que
Ainda não sabemos quem é a força normal! Vamos fazer isso no próximo passo!
Passo 5
Usando a equação e como vimos antes que , temos que
e, portanto, temos que
e, a velocidade, toma então o seguinte formato
ou, simplesmente
Por quê esta é a velocidade máxima? Quando garantimos que o movimento circular seja uniforme, garantimos que o carro não irá deslizar pela pista nas condições dadas. No entanto, colocamos a força de atrito na direção central, portanto, estamos representando a situação em que o carro está tentando deslizar para cima por conta de sua velocidade e o atrito o mantém! Consegue adivinhar qual será a velocidade mínima? Vem comigo!
Passo 6
Analogamente, a velocidade mínima será agora aquela na qual a baixa velocidade faz o carro querer deslizar para baixo, mas note, que o atrito então segurará este movimento, apontando na direção contrária, ou seja, temos o seguinte esquema
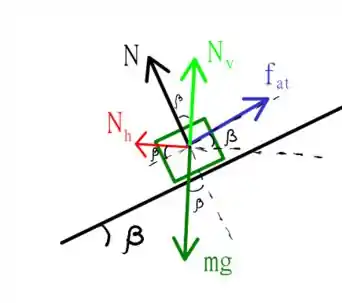
e, da mesma forma que fizemos antes, obteremos a seguinte equação
e a velocidade mínima é simplesmente
o intervalo de velocidades é então dado por
A questão foi isso! Te vejo na próxima! Tchau Tchau!