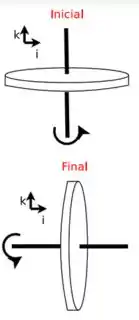
Um disco de raio e massa gira livremente com velocidade angular em torno de um eixo vertical que passa pelo seu centro de massa. Pela ação de um torque, o eixo de rotação é alterado para a horizontal em um intervalo de tempo , conforme a figura abaixo. Sabendo que o módulo da velocidade angular do disco manteve-se constante durante a aplicação do torque, mostre que o módulo do torque médio aplicado é dado por:

Bom, a ideia principal é usarmos o teorema do momento angular. Para isso precisamos calcular qual a variação de momento angular envolvida nessa mudança da direção de giro do disco.

Podemos dizer que:

Mas, temos:

Precisamos então calcular três coisas: .

Começando pelo momento de inércia, como trata-se de um disco, podemos afirmar que:

Já para os vetores velocidade angular, devemos observar a imagem mostrada no enunciado. Inicialmente, o disco girava com velocidade angular na direção e módulo . Após a mudança na direção ele passou a girar na direção com o mesmo módulo.

Assim:

Juntando tudo, vamos ter:

Como estamos interessados no módulo, teremos:

Muito bom!

Agora que já calculamos o módulo da variação do momento angular, podemos chamar o teorema do momento angular:

Isolando o torque médio aplicado, chegamos a:

Olha que coincidência...

Essa é justamente a expressão que o enunciado havia nos pedido para provar!

Portanto, concluímos a demonstração 😊

Conseguiram entender tudo direitinho? Responde Aí!