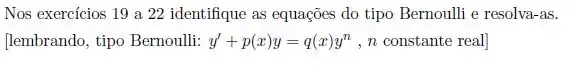Exercícios de Equação de Bernoulli - Lista de Exercícios Resolvida

Identifique que tipo de equação é essa e resolva

Resolva a equação diferencial de Bernoulli

Resolva a equação diferencial de Bernoulli

Resolva a equação diferencial dada sujeita à condição inicial indicada

Resolve o seguinte problema de valor inicial:

Resolva a equação no intervalo :

Encontre todas as soluções da EDO:

Nos exercícios a identifique as equações do tipo Bernoulli e resolva-as. [lembrando, tipo Bernoulli: , constante real]

Nos exercícios a identifique as equações do tipo Bernoulli e resolva-as. [lembrando, tipo Bernoulli: , constante real]

Encontre todas as soluções da EDO:

Encontre todas as soluções da EDO

Resolva as seguintes equações diferenciais ou problemas de valor inicial, conforme seja o caso.

d)

Considere a equação de Bernoulli para :

Divida a equação por e substitua , obtendo uma equação linear em , mas antes verifique se é uma solução;

Resolva a equação linear (obtida acima) para ;

Obtenha a solução em .

Considere a equação de Bernoulli para :

Divida a equação por e substitua , obtendo uma equação linear em ; (Dica: verifique se é uma solução.)

Resolva a equação linear para e obtenha a solução da equação original em .

Resolva a seguinte equação diferencial ou problema de valor inicial conforme caso abaixo:

Encontre a solução geral da equação abaixo:

Questão 1: Resolva as seguintes equações diferenciais e problemas de valor inicial, conforme seja o caso:

2) Resolva o problema de valor inicial, , para EDO

(5pts) Responda verdadeiro (V) ou falso (F) para as seguintes questões:

( ) é resolvível por fator integrante e tem solução geral dada por

;

( ) é linear de ordem 2;

( ) é separável;

( ) A solução satisfaz 1

( ) A solução geral de é dada implicitamente por ;

1Note que essa é uma equação de Bernoulli

Nos exercícios a identifique as equações do tipo Bernoulli e resolva-as. [lembrando, tipo Bernoulli: , constante real]

Considere a problema de valor inicial

Determine sua solução geral analiticamente. Justifique detalhadamente os passos de sua solução.

Resolva esse PVI no Mathematica. Exiba o gráfico da solução superposto ao campo de direções dessa equação diferencial.

4) Suponha que uma certa população tem uma taxa de aumento que satisfaz a equação

Se , determine o prazo , após o qual a população duplicará, .

Resolva o PVI

Resolve as seguintes equações diferenciais. No caso da letra a), resolve o problema de valor inicial associado.

Resolva o problema de valor inicial

Mostre que a seguinte equação é de Bernoulli e indique qual a substituição (i.e. mudança de variável) que a torna linear. Resolva-a pelo método de Bernoulli

Considere uma equação diferencial da forma

Supondo que é uma solução da equação diferencial, fa��a a mudança de variáveis , afim de obter a equação de Bernoulli: