Calcule a área de uma lado da superfície cuja base é a circunferência , no plano , e a altura em cada ponto é .
Passo 1
Aqui a gente precisa achar a área de uma superfície, mas o que isso tem a ver com integral de linha? Na verdade, tudo! Vamos ver como é essa superfície aí:
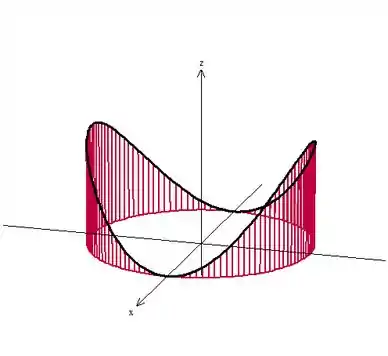
Ou seja, a gente pode dizer que a superfície é a área entre uma função e aquela circunferência da base. E assim como para integrais unidimensionais que representam a área entra a função e o eixo, podemos interpretar a área entre uma função e a curva como um a integral de linha!
O que vamos ter, então, é essa fórmula:
Onde vai ser a circunferência e .
Passo 2
Vamos começar parametrizando a curva, que é uma circunferência de raio , então podemos parametrizá-la assim:
E o módulo do vetor tangente fica:
Tranquilo, agora vamos só substituir tudo na fórmula.
Passo 3
Já temos tudo o que precisamos, então é só jogarmos na fórmula:
Vamos lembrar que :
Pronto, tudo feito!
Resposta
![]()