UTFPR, Sem Campus, Cálculo Diferencial e Integral 3, AV1 - 2022.1, Questão 2
Calcule a integral de linha onde é a metade inferior da circunferência .
Passo 1
Eaew, tudo bem?
O enunciado pede para que calculemos a seguinte integral de linha
ao longo da curva dada pela seguinte circunferência
Mas como fazemos isso? Vamos lembrar que para calcular uma integral de linha, é necessário utilizar uma parametrização da curva e aplicar a seguinte definição
em que é a parametrização da nossa curva, dada por
Belezinha? Vamos tentar resolver este problema agora! Vem comigo!
Passo 2
A primeira coisa que precisamos fazer é parametrizar a nossa curva, uma circunferência é parametrizada sempre da mesma maneira, temos que
em que é o raio da circunferência. Em nosso caso, podemos identificar que , já que a expressão da circunferência é tal que
Portanto, a nossa curva é
Ótimo! Agora, precisamos calcular o módulo da derivada desta curva, e encontrar os limites de integração adequados! Vamos lá!
Passo 3
Primeiro, temos que
Temos que e que , portanto, a derivada de nossa curva é
Agora, qual é o módulo da derivada? O módulo de uma curva com dois componentes é tal que
Colocando o em evidência e usando que , obtemos simplesmente que
Maravilha! Temos quase tudo que precisamos para resolver a nossa integral! Vamos determinar os limites de integração agora!
Passo 4
Temos que a nossa curva é a metade inferior de uma circunferência, ou seja
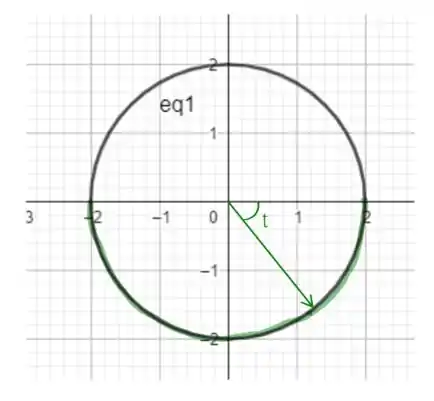
Como faz o papel do ângulo, note que a nossa curva começa em e vai até , portanto, usando tudo que calculamos até agora e essa informação, a integral que precisamos resolver é
Que pode ser divida em duas integrais da forma
Agora é utilizar os métodos de cálculo 1, vamos lá!
Passo 5
Primeiro, lembrando a seguinte primitiva
Como , temos que
Agora, vamos trabalhar a segunda integral! Quando temos um produto de seno e cosseno, como acima, podemos usar substituição simples, chamando o termo com maior potência de , temos que
e
usando então que , temos a seguinte integral
Lembra como se resolve esse tipo de integral? Vem comigo!
Passo 6
Primeiro, usando que e que , temos que
Integrais de polinômios podem ser identificadas como a seguinte primitiva
Avaliando então os limites de integração, temos que
Ou seja, temos que
De forma que com o resultado das duas integrais obtidas, temos que a integral original é
A questão foi isso! Te vejo na próxima! Tchau Tchau!