- Calcule de a , ao longo
- do arco de circunferência , orientada no sentido anti-horário.
Passo 1
Bem, antes do começarmos qualquer coisa, vamos colocar essa integral de linha de uma forma mais elegante.
Como você já pode notar, a integral de linha está assim , certo? Só que esse formato é apenas outra forma de falar que estamos trabalhando uma integral de linha de um campo de vetores:
Onde esse é o vetor...
Se buscamos a solução dessa integral de linha do modo diretão, nada mais justo que seguirmos o passo a passo maroto de resolução desse tipo de integral:
- Parametrizar a curva que estamos trabalhando.
- Substituir os termos do campo vetorial pelos termos da parametrização.
- Encontrar o termo .
Então vem comigo nessa aventura! :D
Passo 2
Vamos então parametrizar a curva , mas por falar nisso, quem é a curva ?
Bem, pelo próprio enunciado, sabemos que a curva que une esses dois pontos está sobre a circunferência de raio deslocada de uma unidade em , ...
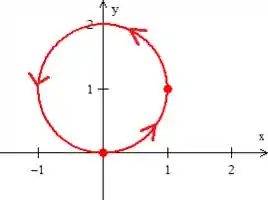
Só que só queremos esse arco aqui oh:
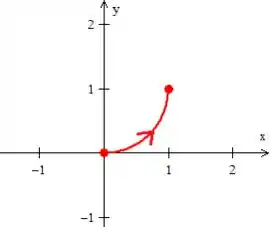
Pois ele é o arco que atende as condições de estar girando no sentido anti-horário e também saindo da origem e chegando lá em cima, saca?
Se a circunferência estivesse centrada na origem, a parametrização seria aquela, a prima das coordenadas polares, se lembra?
Mas, a circunferência está deslocada em de uma unidade, então...
O raio da circunferência é ...
E basicamente terminamos a parametrização. Só que é legal deixa-la de uma forma mais gentil e apresentável, neh? Por isso falamos que a parametrização é
Passo 3
Nunca devemos concluir uma parametrização sem antes dizer onde o parâmetro, no caso , varia.
Nesse caso, note que o gira da origem até o ponto :
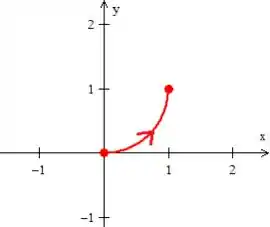
Na origem, , então...
Dois candidatos de ângulos que dão o cosseno são
pra saber qual dos dois estamos falando, usemos o também...
Epa! o seno é negativo, então o que queremos saindo da origem é
Usando os mesmos raciocínios para os o outro ponto, , ...
Repare que, nesse caso, só pode ser , afinal de contas a curva gira aumentando o ângulo no sentido anti-horário!
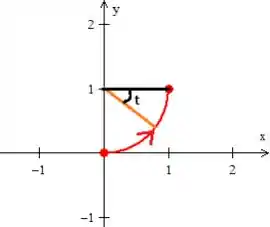
Logo...
Passo 4
Beleza! Agora devemos prosseguir substituindo no campo vetorial , esse e pelos termos da parametrização:
Lembrando que e ...
Passo 5
Para encontrar o termo , basta sabermos que facilmente o encontramos fazendo:
Como no caso a parametrização foi , derivando cada termo do vetor em relação a ...
Logo...
Passo 6
Voltando para a integral de linha que estamos trabalhando
e substituir todos os dados que obtivemos...
Não se esqueça de realizar esse produto escalar de vetores aí, heim!
Vamos calcular essas integrais separadamente!
Passo 7
Em relação a primeira integral... ...
podemos fazer uma substituição do tipo
não esqueça dos limites
Passo 8
Com relação a ... Lembre-se que ...
como ...
Passo 9
Vamos agora para a última integral e é a cereja do nosso bolo, afinal, é uma integral direta!
Passo 10
Somando o resultado das três: