Considere a função
Determine o seu domínio, os intervalos de crescimento e decrescimento, estude e classifique os pontos críticos (se existirem), estude as concavidades e classifique os pontos de inflexão (se existirem), determine as assíntotas (verticais, horizontais e/ou oblíquas), e esboce o gráfico de .
Passo 1
Fala aí, pessoal! Essa questão nos pediu um monte de coisas diferentes, então vamos começar pelo Domínio. Lembrando que domínio são os valores que pode assumir.
Olhando para a nossa função, quais são os valores que não pode assumir?
Nesse caso, nossa única limitação é que não podemos zerar o denominador:
Logo, os valores que não pode assumir são:
Então nosso domínio são todos os números reais menos esses dois:
Passo 2
Agora que já falamos sobre o domínio, está na hora de falar sobre crescimento e decrescimento.
O que precisamos lembrar é que quem dita esses intervalos é a primeira derivada:
- Se
- Se
- Se
- Se
Vamos calcular a primeira derivada da nossa função:
Como temos uma função de no numerador e outra no denominador, temos que usar a Regra do Quociente:
Fazendo isso no nosso caso, teremos:
Fazendo essas derivadas:
Fazendo essas multiplicações no numerador:
Agora que temos a primeira derivada, temos que analisar os pontos críticos, ou seja, pontos onde a derivada é igual a zero ou não existe! E porque vamos fazer isso? Porque são os pontos críticos que separam os trechos em que a função é crescente ou decrescente.
Bom, a derivada será zero quando o numerador for zero, então:
Logo o único valor de que leva esse numerador a zero, é o próprio:
Agora pontos onde a derivada não existe, são pontos que anulam o denominador:
Os valores de que levam esse denominador a zero são:
Mas como você deve lembrar do Passo , esses valores não são parte do domínio de , então eles não podem ser pontos críticos! Apenas o é um ponto crítico.
Passo 3
Relembrando, se a função tiver trechos crescente e decrescentes, o ponto crítico separa esses trechos. Por isso que calculamos esse ponto.
Então agora, vamos estudar dois intervalos: antes e depois do ponto crítico, ou seja, de até e de até .
Nós temos que descobrir, pra valores positivos e negativos de , qual vai ser o sinal da derivada da função.
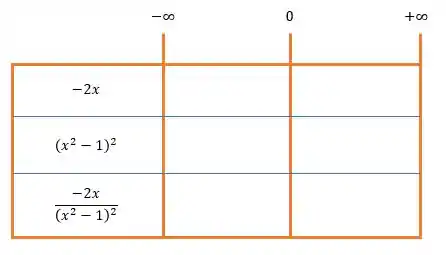
Olhando apenas para o numerador:
Quando substituímos por valores negativos, ou seja , o numerador será um número positivo.
Enquanto o denominador:
Substituindo por números negativos, esse denominador será positivo também, pois o termo está inteiro elevado ao quadrado. Na verdade, esse denominador sempre será positivo, independente do valor de !
Logo dividindo um número positivo por outro número positivo, encontraremos um número positivo!

Agora quando substituímos o numerador por números positivos, como temos um sinal de menos na frente dele, ele se tornará um número negativo.
Enquanto o denominador, quando substituímos o valor de por um valor positivo, ele continua sendo positivo!
Então se dividimos um valor negativo por um número positivo, encontraremos sempre um valor negativo:
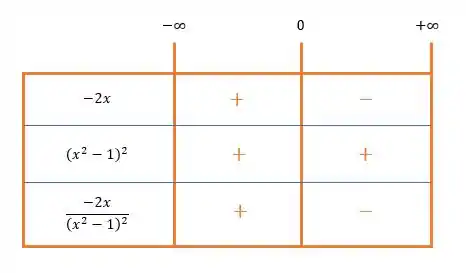
Relembrando nossa regra:
Assim, percebemos que no intervalo , nossa função é crescente, enquanto no intervalo de , nossa função é decrescente!
Passo 3
Agora desejamos estudar a concavidade da função e para isso usamos o Teste da Segunda Derivada, ou seja:
- Se
- Se
Nossa primeira derivada vale:
Temos que usar a Regra do Quociente mais uma vez:
Fazendo as derivadas separadamente:
Enquanto para essa derivada , precisaremos usar a Regra da Cadeia:
Então:
Podemos cortar o que está presente tanto no numerador quanto no denominador:
Simplificando o numerador, nós temos:
Antes de olharmos para a concavidade, vamos identificar os pontos de inflexão, ou seja, pontos que tornam a Segunda Derivada igual a zero:
Para isso, o numerador da Segunda Derivada precisa ser igual a zero:
Percebe que não temos nenhuma raiz real, logo não temos nenhum ponto de inflexão!
Passo 4
Agora vamos voltar a nossa concavidade, a Segunda Derivada é:
Você concorda comigo que o numerador é sempre positivo:
Porque independentemente do valor de , como ele será elevado ao quadrado, ele se tornará positivo. Então precisamos analisar o valor do denominador:
Concorda comigo que se o valor de for menor que , teremos um valor negativo elevado ao cubo e continuará negativo? Logo:
Então se o valor de estiver entre e , nós teremos um denominador negativo e consequentemente, uma Segunda Derivada sempre negativa:
Enquanto se tivermos um valor de maior que ou menor que , teremos um denominador positivo:
Como o denominador é positivo, então a Segunda Derivada também é maior que zero:
Relembrando: quando a Segunda Derivada é positiva, a concavidade é para cima, enquanto a Segunda Derivada é negativa, a concavidade é para baixo. Logo:
Passo 5
Agora queremos estudar as assíntotas verticais, que são pontos de descontinuidade, em que a função tende a ou . Então, temos que estudar o limite quando nos aproximamos de valores que estão fora do nosso domínio, ou seja, e .
Começando por :
Vamos fazer o limite pelo outro lado:
Como fazendo o limite dos dois lados de , chegamos no valor de , então ele é uma assíntota vertical!
Agora vamos estudar o limite pelos dois lados de :
Vemos que de novo, o limite é igual a pelos dois lados de , então ele também é uma assíntota vertical!
Passo 6
Agora vamos estudar as assíntotas horizontais. Pra isso, aplicamos o limite para e , e vemos se isso dá um valor real.
Nesse caso, se fizermos , vamos cair em uma indeterminação. Então vamos colocar o nosso do denominador em evidência, porque que a gente reescreve as funções a gente as vezes consegue fugir das indeterminações.
Ótimo! Como chegamos a um valor, então temos uma assíntota horizontal!
Vamos fazer o limite aproximando de :
Confirmamos que é uma assíntota horizontal, tanto para tendendo para mais infinito e menos infinito.
Passo 7
Juntando todas as informações sobre concavidade e assíntotas verticais e horizontais, encontramos o seguinte gráfico:
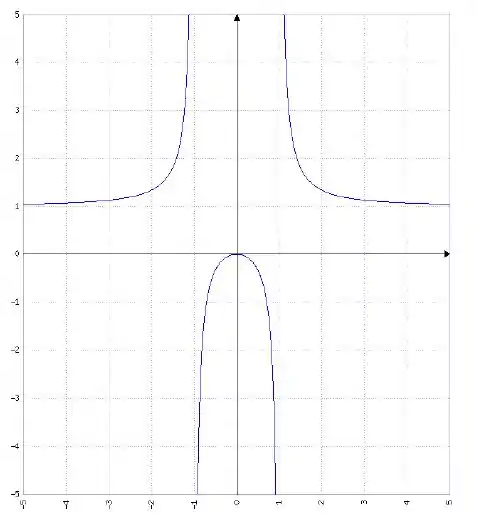
Resposta
Ei, a resposta está no passo a passo :)