Seja .
(a) Determine os intervalos de crescimento/decrescimento de , e os seus pontos de máximo/mínimo.
(b) Determine os intervalos onde é côncava para cima/baixo e os seus pontos de inflexão.
(c) Caso existam, encontre as assíntotas horizontais e verticais de .
(d) Esboce o gráfico de usando (pelo menos) as informações obtidas nos itens (a), (b) e (c).
Passo 1
Então pessoal, essa é uma questão muito importante, então vamos juntos resolvê-la passo a passo.
(a) Pra encontrar os intervalos de crescimento ou decrescimento, temos que olhar par o sinal da derivada da função.
Então primeiro vamos calcular essa derivada:
E aí temos que usar a regra do produto:
A derivada de é mesmo! E a derivada de é , então:
Ok, agora vamos dar uma olhada no sinal dessa função.
Passo 2
Quando essa derivada é maior do que zero?
Dividindo os dois lados por :
Quando a derivada é maior do que zero, a função é crescente, e vice-versa, então:
E quando ?
Então temos um ponto crítico nesse ponto. Já vamos descobrir se é um máximo ou mínimo.
Passo 3
(b) Para descobrir a concavidade dessa função, temos que calcular a derivada segunda:
A derivada de é mesmo, e o segundo termo ali é exatamente a derivada que a gente calculou no passo anterior, então:
Agora vamos pensar no sinal dessa função:
Mais uma vez, vamos dividir por dos dois lados:
Quando a derivada segunda é maior do que zero, a concavidade é para cima, e vice-versa, então:
E quando a derivada segunda é zero, ou seja, temos um ponto de inflexão em .
Passo 4
E agora a gente já tem informação suficiente pra classificar aquele ponto crítico que achamos em .
Como a concavidade é voltara para cima em , então o ponto crítico em é um ponto de mínimo.
Só pra lembrar, a regra pra classificar os pontos críticos é essa aqui:
Passo 5
(c) O próximo passo é encontrar as assíntotas horizontais e verticais.
O primeiro passo pra fazer isso é ver o que acontece nos limites quando .
No caso do , as duas funções “explodem”, e então o limite é . Isso quer dizer que não temos uma assíntota nesse ponto.
E quando , a coisa complica um pouco:
Se a gente arrumar ou pouco essa função, dá pra aplicar a regra de L’Hospital:
Beleza, agora tanto o numerador quanto o denominador tendem ao infinito, então dá pra aplicar a regra. Para isso, temos que derivar as duas funções:
Então:
Agora sim, quando tende a , essa função vai tender a zero.
Ou seja, temos essa situação aqui:
A função tende a um valor finito quando tende a . Então temos uma assíntota horizontal em quando .
Passo 6
Será que temos alguma assíntota vertical? Bom, esse tipo de assíntota aparece nesse caso aqui:
Ou seja, quando a função tende a um valor infinito quando tende a um valor finito.
Vamos olhar pra nossa função:
Ela só explode nos extremos , então não temos nenhuma assíntota vertical.
Passo 7
Então tá, agora chegou a hora de esboçar o gráfico, vamos listar tudo que a gente descobriu até aqui:
Beleza, com isso já dá pra desenhar o gráfico. Uma boa ideia é seguir esses passos aqui:
1. Perceba que o gráfico cruza a origem, porque .
2. Desenhe uma curva com crescimento exponencial a partir do até o . Sabendo que a função tem um valor pequeno e negativo em .
3. Desenhe uma curva com decrescimento exponencial a partir do , e que faz uma assíntota no eixo horizontal quando . Com o ponto de mínimo em .
4. Nessa curva aí do passo 2, deixe o ponto de inflexão (quando a concavidade “vira” de sentido), no ponto .
Beleza, com isso você já deve chegar em um gráfico como esse aqui:
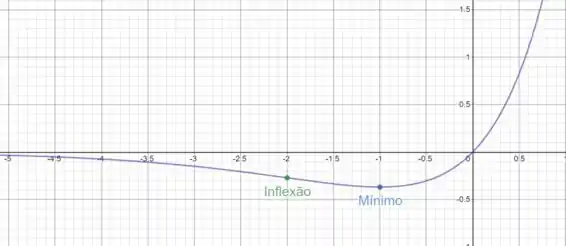
Resposta
(a) A função é crescente em e decrescente em . Tem um ponto de mínimo em .
(b) A função é côncava para cima em e côncava para baixo em . Tem um ponto de inflexão em .
(c) A função tem uma assíntota horizontal em quando tende a .
(d) Ver esboço.