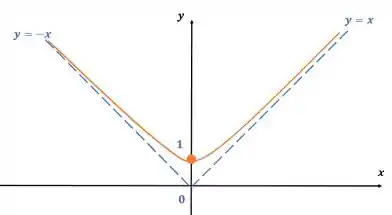
Para a seguinte função:
Encontre as assíntotas inclinadas e esboce o gráfico, e para isso:
- Encontre os intervalos para os quais a função é crescente ou decrescente;
- Encontre os valores de máximo e mínimo locais;
- Encontre os intervalos de concavidade e os pontos de inflexão;
- Encontre as assíntotas horizontais e verticais e inclinadas;
- Esboce o gráfico, utilizando as informações dos itens anteriores
Passo 1
Fala aí, amigão! O enunciado é longo, mas tudo isso vai nos ajudar a completar o nosso gráfico final. Então mãos à obra!
Nossa função é:
Nosso primeiro passo é encontrar os intervalos para os quais essa função é crescente e quais ela é decrescente.
Então vamos usar a Regra da Primeira Derivada!
Vamos começar reescrevendo:
Derivando:
Logo a primeira derivada pode ser reescrita como:
Agora precisamos encontrar quais valores onde nossa primeira derivada é igual a zero!
Então:
Por outro lado, o valor do denominador nunca muda de sinal, ele é sempre positivo!
Vamos colocar esses valores no quadro de sinais:
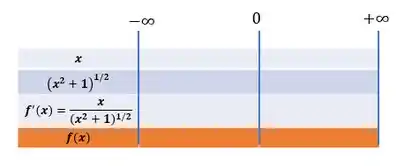
Agora analisando os valores que cada parcela assume dentro dos intervalos, temos que a função ( assume os seguintes sinais:
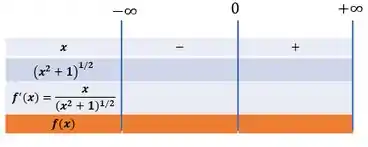
Enquanto a função sempre assume valores positivos:
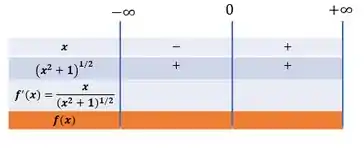
Dividindo essas parcelas, podemos concluir sobre o sinal que a derivada da função assume em cada um dos intervalos é:
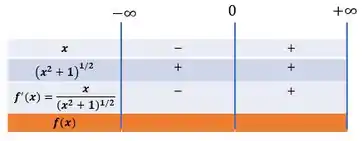
E o que sabemos através da Regra da Primeira Derivada:
- Se , então é crescente nesse intervalo;
- Se , então é decrescente nesse intervalo.
Então, através do nosso quadro de sinais chegamos a resposta do primeiro item:
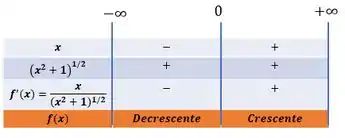
é crescente no intervalo:
é decrescente no intervalo:
Passo 2
Já achamos a primeira resposta, hora de olha para o segundo pedido de nossa questão, na letra “b”, o enunciado nos diz para encontrar os valores de máximo e mínimo locais. Para isso, vamos usar um pouco do que já construímos no item anterior!
Quando ocorre o ponto de máximo ou ponto de mínimo? Bom, isso ocorre quando a derivada primeira de uma função é igual a zero!
No último passo, descobrimos que isso ocorre quando:
Como sabemos que a função é decrescente de até e depois ela começa a crescer, então:
Passo 3
Na letra “c”, o enunciado nos pede para encontrar os pontos de inflexão e a concavidade que a função assume. E como começamos isso? Teste da Segunda Derivada!
Se a nossa primeira derivada vale:
Para encontrar a segunda derivada, vamos usar a Regra do Quociente:
Por fim chegamos a:
Pela Regra da Segunda Derivada, temos:
- Se , então tem concavidade para cima nesse intervalo;
- Se , então tem concavidade para baixo nesse intervalo.
- Intervalos de Crescimento e Decrescimento:
- Pontos de Mínimo:
- Concavidade:
- Assíntotas Oblíquas:
E como vamos avaliar esse sinal? Bom o denominador é sempre positivo, pois está elevado ao quadrado e somado ao número .
Por outro lado, o numerador apresenta também sempre é positivo igual a . Logo, a concavidade é sempre para cima!
Passo 4
A letra “d” é: Encontre as assíntotas horizontais e verticais e inclinadas.
Começando pela assíntota horizontal:
Agora para o outro lado:
Logo, não temos nenhuma assíntota horizontal!
Partindo para assíntotas verticais, vamos ver onde temos uma descontinuidade! No caso da nossa função:
Nós não temos nenhuma descontinuidade, logo não existe nenhuma assíntota vertical!
Como não existem assíntotas horizontais, vamos ter que testar as assíntotas inclinadas, também chamadas de assíntotas oblíquas!
Vamos começar testando para :
O coeficiente é calculado como:
Substituindo a nossa função:
Para resolver esse limite, saca só esse conceito importante:
Como estamos trabalhando com , então:
Vamos colocar todos os termos dentro da raiz:
Então chegamos no limite final:
E calculando o coeficiente :
Substituindo nossos valores:
Devemos multiplicar pelo conjugado:
Então agora está na hora de aplicar esses valores na função da assíntota oblíqua:
Então, temos a seguinte assíntota oblíqua pro lado de :
Vamos aplicar o mesmo passo a passo para o lado de :
Calculando o coeficiente :
Substituindo a nossa função:
Vamos colocar todos os termos dentro da raiz:
Então chegamos no limite final:
E calculando o coeficiente :
Substituindo nossos valores:
Precisamos multiplicar pelo conjugado:
Ficamos com:
Que resulta em:
Então agora está na hora de aplicar esses valores na função da assíntota oblíqua:
Então, temos a seguinte assíntota oblíqua pro lado de :
Passo 5
E por último, vamos esboçar esse gráfico, nos baseando em todas as informações que nós levantamos anteriormente.
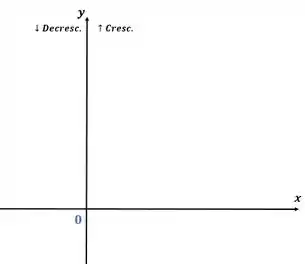
Substituindo na função:
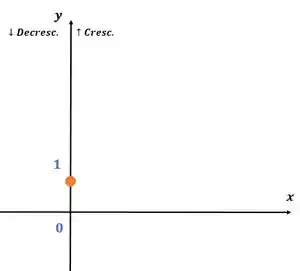
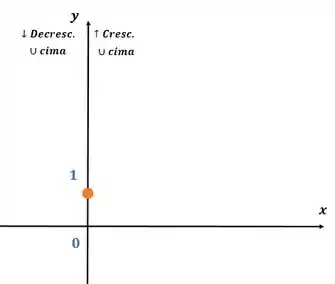
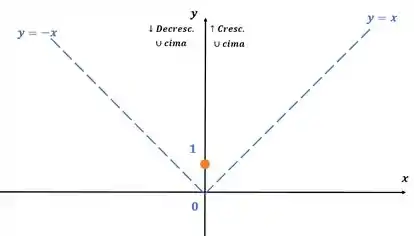
Por fim, temos o seguinte gráfico:
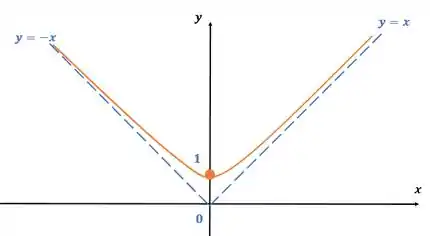
Resposta
-
é crescente no intervalo:
é decrescente no intervalo: