Para a próxima função:
- Encontre os intervalos para os quais a função é crescente ou decrescente;
- Encontre os valores de máximo e mínimo locais;
- Encontre os intervalos de concavidade e os pontos de inflexão;
- Encontre as assíntotas horizontais e verticais;
- Esboce o gráfico, utilizando as informações dos itens anteriores.
Passo 1
Fala aí, amigão! Temos um passo a passo que vai nos ajudar a construir no final o nosso gráfico, beleza? Então mãos a obra!
Nossa função é:
Nosso primeiro passo é encontrar os intervalos para os quais essa função é crescente e quais ela é decrescente. E como fazemos isso? Se você respondeu Regra da Primeira Derivada, você ACERTOU!
Então vamos derivar essa função ). Aplicando no nosso caso:
Agora precisamos encontrar quais valores onde nossa primeira derivada é igual a zero!
Então:
Logo, o valor é igual a:
Vamos analisar todos os pontos possíveis para o seno e colocar esses valores no quadro de sinais:
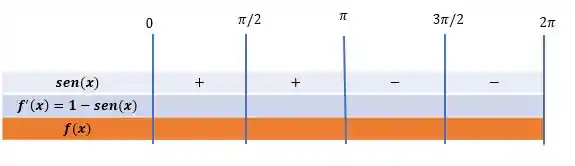
O valor máximo que o seno pode assumir é igual:
Por esse motivo:
Então o sinal da primeira derivada sempre será positivo:
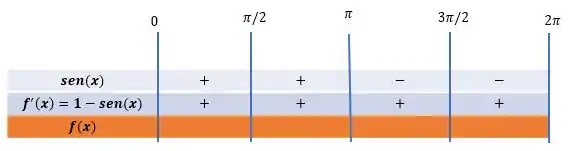
E o que sabemos através da Regra da Primeira Derivada:
- Se , então é crescente nesse intervalo;
- Se , então é decrescente nesse intervalo.
Então, através do nosso quadro de sinais chegamos a resposta do primeiro item:
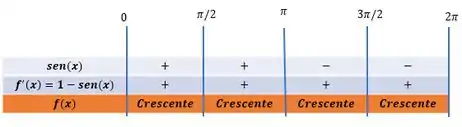
Como a função seno é uma função periódica, então podemos replicar o que acontece no intervalo de a para todo intervalo :
é crescente no intervalo:
Passo 2
Já achamos a primeira resposta, hora de olha para o segundo pedido de nossa questão, na letra “b”, o enunciado nos diz para encontrar os valores de máximo e mínimo locais. Para isso, vamos usar um pouco do que já construímos no item anterior!
Quando ocorre o ponto de máximo ou ponto de mínimo? Bom, isso ocorre quando a derivada primeira de uma função é igual a zero!
No último passo, descobrimos que isso ocorre quando:
Então no intervalo , o valor de mínimo local ocorre em .
Porém no intervalo de , o valor mínimo ocorre diversas vezes na posição:
Passo 3
Na letra “c”, o enunciado nos pede para encontrar os pontos de inflexão e a concavidade que a função assume. E como começamos isso? Teste da Segunda Derivada!
Se a nossa primeira derivada vale:
Pela Regra da Segunda Derivada, temos:
- Se , então tem concavidade para cima nesse intervalo;
- Se , então tem concavidade para baixo nesse intervalo.
- Intervalos de Crescimento e Decrescimento:
- Pontos de Máximo:
- Pontos de Mínimo:
- Concavidade:
- Assíntota vertical:
- Assíntota Oblíqua:
Vamos colocar os valores que pode assumir no quadro de sinais:
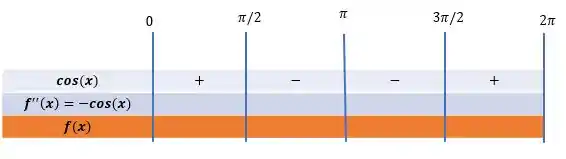
Dessa forma, o sinal da segunda derivada será:
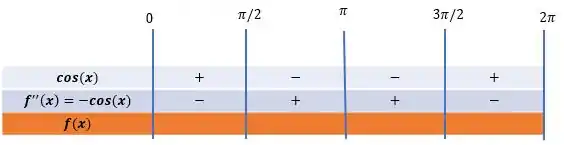
Podemos concluir sobre a concavidade da função:
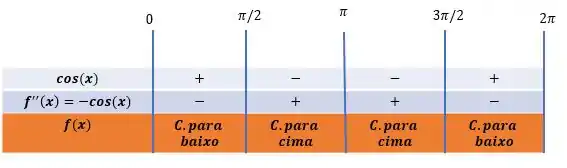
E o ponto de inflexão? É onde segunda derivada é igual a zero:
Como isso se repete em todo o intervalo de , então os pontos serão:
Passo 4
A letra “d” é: Encontre as assíntotas horizontais e verticais e inclinadas.
Começando pela assíntota horizontal:
Como cosseno sempre varia de a :
Somando o valor de dos dois lados:
Aplicando os limites dos dois lados:
Chegamos finalmente no limite igual a:
Agora para o outro lado, vamos fazer a mesma coisa:
Como cosseno sempre varia de a :
Somando o valor de dos dois lados:
Aplicando os limites dos dois lados:
Chegamos finalmente no limite igual a:
Dessa forma, não existem assíntotas horizontais!
Partindo para assíntotas verticais, vamos ver onde temos uma descontinuidade! No caso da nossa função:
Você percebe que não existe descontinuidade, por isso não existe assíntota vertical!
Como já falamos que não existem assíntotas horizontais, teremos que testar se existem assíntotas inclinadas, também chamadas de assíntotas oblíquas. Vamos começar testando para :
O coeficiente é calculado como:
Substituindo a nossa função:
Vamos aplicar o teorema do confronto para calcular esse limite, veja:
Dividindo por :
Aplicando o limite:
Chegamos a:
Logo o coeficiente se torna:
E calculando o coeficiente :
Substituindo nossos valores:
Então agora está na hora de aplicar esses valores na função da assíntota oblíqua:
Então, temos a seguinte assíntota oblíqua pro lado de :
Vamos aplicar o mesmo passo a passo para o lado de :
Calculando o coeficiente :
Vamos aplicar o teorema do confronto para calcular esse limite, veja:
Dividindo por :
Aplicando o limite:
Chegamos a:
Logo o coeficiente se torna:
E calculando o coeficiente :
Substituindo nossos valores:
Então, temos a seguinte assíntota oblíqua pro lado de :
Passo 5
E por último, vamos esboçar esse gráfico, nos baseando em todas as informações que nós levantamos anteriormente.
Substituindo na função:
Substituindo na função:
Resposta
-
é crescente no intervalo:
é crescente no intervalo:
-
A concavidade no intervalo é para cima.
A concavidade no intervalo é para baixo.
Não tem pontos de inflexão
Não existem assíntotas horizontais
Assíntota vertical:
Assíntota inclinada: