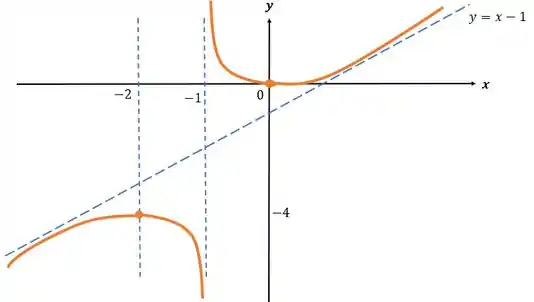
Para a seguinte função:
Encontre as assíntotas inclinadas e esboce o gráfico, e para isso:
- Encontre os intervalos para os quais a função é crescente ou decrescente;
- Encontre os valores de máximo e mínimo locais;
- Encontre os intervalos de concavidade e os pontos de inflexão;
- Encontre as assíntotas horizontais e verticais e inclinadas;
- Esboce o gráfico, utilizando as informações dos itens anteriores
Passo 1
Fala aí, amigão! Temos um passo a passo que vai nos ajudar a construir no final o nosso gráfico, beleza? Então mãos a obra!
Nossa função é:
Nosso primeiro passo é encontrar os intervalos para os quais essa função é crescente e quais ela é decrescente. E como fazemos isso? Se você respondeu Regra da Primeira Derivada, você ACERTOU!
Então vamos derivar essa função , como você deve ter percebido, temos uma fração entre duas expressões, então vamos usar a regra do quociente aqui:
Aplicando no nosso caso:
Logo a primeira derivada pode ser reescrita como:
Agora precisamos encontrar quais valores onde nossa primeira derivada é igual a zero!
Então:
Temos duas opções para tornar essa igualdade verdadeira:
Vamos colocar esses valores no quadro de sinais:
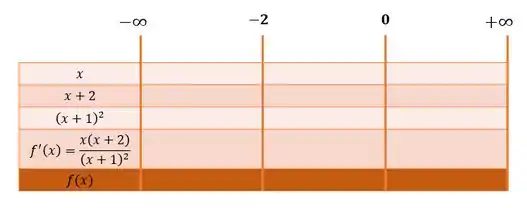
Agora analisando os valores que cada parcela assume dentro dos intervalos, temos que a função assume os seguintes sinais:
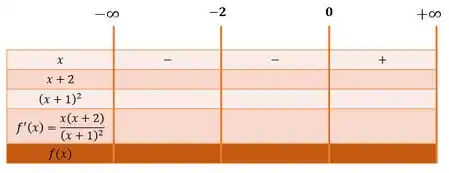
Enquanto a função só assume valores negativos para valores de menores do que :
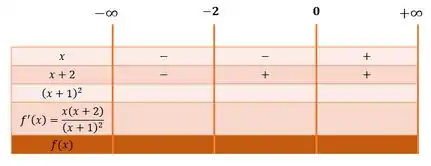
Como a função que está presente no denominador está elevado ao quadrado, então ela é sempre positiva independentemente do valor de :
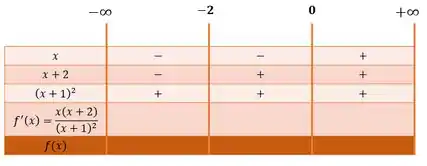
Multiplicando e dividindo essas parcelas, podemos concluir sobre o sinal que a derivada da função assume em cada um dos intervalos é:
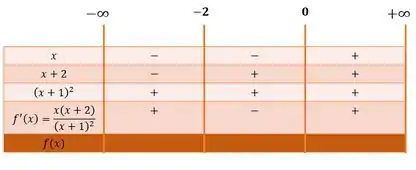
E o que sabemos através da Regra da Primeira Derivada:
- Se , então é crescente nesse intervalo;
- Se , então é decrescente nesse intervalo.
Então, através do nosso quadro de sinais chegamos a resposta do primeiro item:
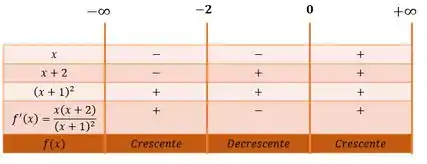
é crescente no intervalo:
é crescente no intervalo:
Passo 2
Já achamos a primeira resposta, hora de olha para o segundo pedido de nossa questão, na letra “b”, o enunciado nos diz para encontrar os valores de máximo e mínimo locais. Para isso, vamos usar um pouco do que já construímos no item anterior!
Quando ocorre o ponto de máximo ou ponto de mínimo? Bom, isso ocorre quando a derivada primeira de uma função é igual a zero!
No último passo, descobrimos que isso ocorre quando:
Como sabemos que a função é crescente de até e depois ela começa a decrescer, então:
Enquanto por outro lado, se a função é decrescente de até e depois ela retorna a crescer até o final , logo:
Essa é a nossa resposta sobre quem são os pontos de máximo e mínimo locais!
Passo 3
Na letra “c”, o enunciado nos pede para encontrar os pontos de inflexão e a concavidade que a função assume. E como começamos isso? Teste da Segunda Derivada!
Se a nossa primeira derivada vale:
Para encontrar a segunda derivada, vamos usar a Regra do Quociente:
Subtraindo uma expressão da outra no numerador:
Por fim chegamos a:
Pela Regra da Segunda Derivada, temos:
- Se , então tem concavidade para cima nesse intervalo;
- Se , então tem concavidade para baixo nesse intervalo.
- Se :
- Se :
- Intervalos de Crescimento e Decrescimento:
- Pontos de Máximo:
- Pontos de Mínimo:
- Concavidade:
- Assíntota vertical:
- Assíntota Oblíqua:
E como vamos avaliar esse sinal? Bom o numerador é sempre positivo e igual a dois, então quem vai definir o sinal é o sinal do denominador:
Logo, teremos o sinal da segunda derivada também é positivo:
Então a concavidade no intervalo é para cima!
Logo, teremos o sinal da segunda derivada também é negativo:
Então a concavidade no intervalo é para baixo!
E o ponto de inflexão? Bom como a derivada segunda nunca é igual a zero:
Então esse ponto de inflexão não existe!
Passo 4
A letra “d” é: Encontre as assíntotas horizontais e verticais e inclinadas.
Começando pela assíntota horizontal:
Se substituirmos o valor de , teremos a indeterminação , logo aplicamos a Regra de L’Hospital:
Agora para o outro lado:
Nesse caso, temos a indeterminação , vamos aplicar L’Hospital novamente:
Dessa forma, não existem assíntotas horizontais!
Partindo para assíntotas verticais, vamos ver onde temos uma descontinuidade! No caso da nossa função:
Você percebe que um número que não faz parte do domínio da função é o número , porque isso iria zerar o denominador e isso não pode acontecer!
Logo a assíntota vertical é:
Dessa forma, existe a assíntota vertical:
Como já falamos que não existem assíntotas horizontais, teremos que testar se existem assíntotas inclinadas, também chamadas de assíntotas oblíquas. Vamos começar testando para :
O coeficiente é calculado como:
Substituindo a nossa função:
Podemos então realizar uma simplificação:
Concorda comigo que isso é uma indeterminação do tipo então vamos aplicar L’Hospital:
E calculando o coeficiente :
Substituindo nossos valores:
Caímos na mesma indeterminação , então vamos aplicar L’Hospital:
Então agora está na hora de aplicar esses valores na função da assíntota oblíqua:
Então, temos a seguinte assíntota oblíqua pro lado de :
Vamos aplicar o mesmo passo a passo para o lado de :
Calculando o coeficiente :
Substituindo a nossa função:
Podemos então realizar uma simplificação:
Concorda comigo que isso é uma indeterminação do tipo então vamos aplicar L’Hospital:
E calculando o coeficiente :
Substituindo nossos valores:
Caímos na mesma indeterminação , então vamos aplicar L’Hospital:
Então agora está na hora de aplicar esses valores na função da assíntota oblíqua:
Então, temos a seguinte assíntota oblíqua pro lado de :
Passo 5
E por último, vamos esboçar esse gráfico, nos baseando em todas as informações que nós levantamos anteriormente.
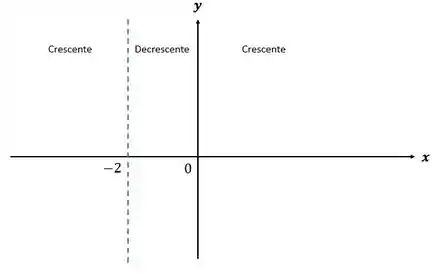
Substituindo na função:
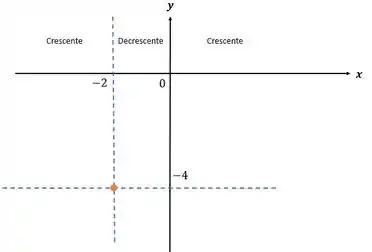
Substituindo na função:
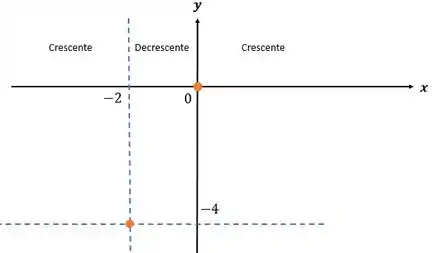
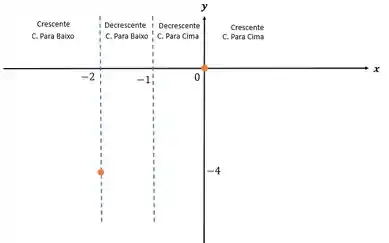
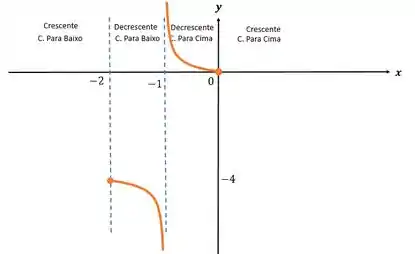
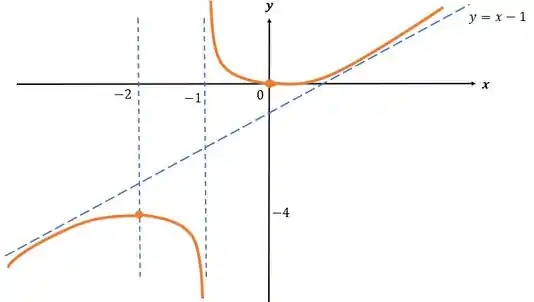
Resposta
-
é crescente no intervalo:
é crescente no intervalo:
-
A concavidade no intervalo é para cima.
A concavidade no intervalo é para baixo.
Não tem pontos de inflexão
-
Não existem assíntotas horizontais
Assíntota vertical:
Assíntota inclinada: