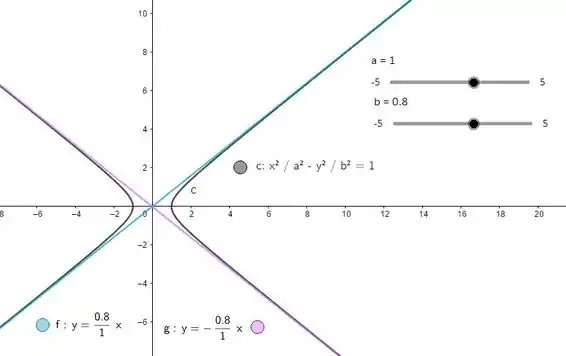
Seja ;
- Determine todas as assíntotas (horizontais, verticais e oblíquas) de , justificando quando não houver
- Determine os pontos de máximo e mínimo, justificando quando não houver
- Esboce o gráfico da curva acima
Passo 1
Essa questão do jeito que tá, enrola um pouco a cabeça. Nesse passo então, vamos desenrolar esse enunciado e escrever . Saca só:
Eita, então teremos duas funções diferentes pra analisar nesse caso! Vamos com calma que chegamos lá.
Passo 2
Para calcular as assíntotas verticais, primeiro temos que ver o domínio das duas que geramos. Como tempos uma raiz, a única forma de isso dar problema é se:
Sendo assim, tem dois pontos interessantes pra gente checar: e . Vamos calcular os limites nesses pontos, bele?
E veja só: em todas as combinações possíveis (temos duas funções, dois pontos pra calcular e duas direções, esquerda e direita, pra calcular o limite) o limite é . Ou seja, não temos assíntotas verticais!
Pra ver as assíntotas horizontais agora, a gente vai fazer o limite pra mais ou menos infinito e ver se a função tende pra um valor ou se cresce cresce cresce e não para. Show, fazendo todas as combinações possíveis (duas funções e dois limites):
Então nenhuma das duas funções tem assíntotas horizontais também!
Passo 3
Vamos lembrar que as assíntotas oblíquas são definidas por:
Então, uma coisa de cada vez se não a gente se afoba. Primeiro achamos , depois . Para a função , o cálculo de vai ficar:
Colocando em evidência:
Aplicando o limite:
Agora vamos calcular o valor de . Felizmente só vamos ter pra nos preocuparmos já que também só achamos . Como , calculamos o da seguinte forma:
Multiplicando pelo conjugado em cima e em baixo:
Agora que não tem nenhum termo com em cima, vemos que independente de se ou se , todo o denominador tende a números infinitamente grandes e, sendo uma constante, esse limite vai a . Logo:
E a assíntota oblíqua de vai ser:
Agora, para a função , o cálculo de e vai ficar bem parecido, quase igual na verdade! Mas pra não deixarmos de fazer, vamos seguir os mesmos passos. Começando por então, temos:
Aplicando o limite:
Para o cálculo de então vamos ter:
E aplicando o limite, chegamos também à . Por fim, obtemos que a assíntota oblíqua de vai ser:
Passo 4
Ok, resolvemos toda a letra , mas falta o resto. Pra falarmos sobre pontos de máximo e de mínimo temos que pensar em pontos críticos. E pra isso, trazemos nosso grande amigo: o deriva e iguala a . Partiu então:
Perceba que o único jeito dessa derivada zerar é se . Mas vai com calma porque não rola. Lembra que não estava definido no intervalo:
Porque geraria uma raiz negativa? Aqui é a mesma coisa! Como:
Passo 5
Show, agora vamos juntar tudo! Temos que a curva:
É a soma de duas funções:
Informações que tiramos:
- Nenhuma das duas funções tem assíntotas horizontais
- Nenhuma das duas funções tem assíntotas verticais
- As assíntotas oblíquas existentes são
- A função não está definida em
- As duas funções interceptam o eixo em
Graficamente, vemos:
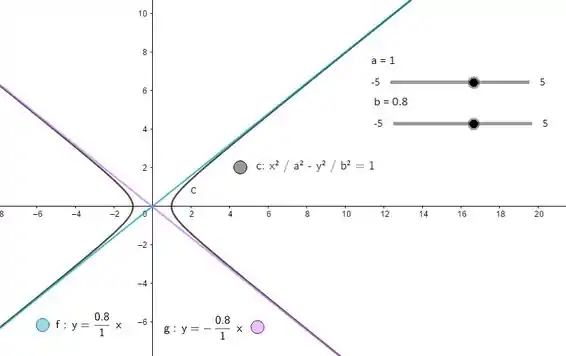
Resposta
- Possui somente assíntotas oblíquas:
- Não possui quaisquer pontos críticos pois
- O gráfico é dado: