Sejam e campos escalares definidos em de classe . Calcule
Passo 1
Primeiro vamos achar os vetores gradientes
Estou usando essa notação porque esse monstro vai crescer absurdamente, então assim é mais fácil de fazer.
Vamos agora ao produto vetorial
Para esse produto vetorial vamos fazer
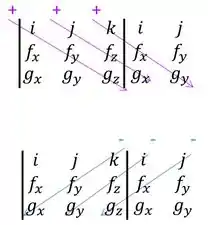
Vai ficar
Isso vai ficar
Passo 2
O divergente dessa parada vai ficar
Vamos usar as propriedades de derivada aqui, lembrando que a derivada do produto é a derivada do primeiro vezes o segundo mais a derivada do segundo vezes o primeiro. Então vamos ter
Vamos fazer cada uma dessas derivadas separado
Ufa, confere tudo aí com calma, porque essa parada é braba mesmo.
O divergente vai ficar
Vamos dar uma ajeitada nessa parada toda, como a ordem de derivação não vai ficar diferente, vamos colocar tudo na ordem alfabética
Vamos escrever junto tudo que temos que é igual para você poder ver melhor isso
Isso tudo dá , então mostramos como ele queria que
Resposta
Ei, a resposta está no passo a passo :)