Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Movimento Circular Acelerado

Ver Teoria
Exercício 123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657

Enunciado

O gráfico a seguir representa a velocidade angular, em função do tempo, de uma polia que gira ao redor de um eixo.

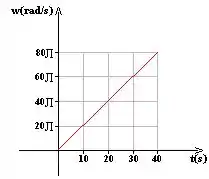
Com base nas informações contidas no gráfico, determine a aceleração angular desta polia e a quantidade de volta que ela dá no intervalo de tempo entre 0 e 40s.

Passo 1

Bom, pra gente calcular a aceleração angular tendo a velocidade angular inicial, final e o tempo, podemos usar a equação da velocidade no movimento circular acelerado! Então:

ω = ω 0 ±   α t

Onde α é a aceleração angular que queremos descobrir! Show! Então vamos usar os dados que a questão nos deu:

80 π = 0 ±   α . 40

α = 2 π   r a d / s 2

Lindíssimo!

Passo 2

Agora que temos a aceleração angular, fica fácil descobrirmos o espaço total percorrido, né?

Vamo lá, nossa equação é:

θ =   θ 0 ± ω 0 t ± α t 2 2

∆ θ = ω 0 t ± α t 2 2

Então, temos:

∆ θ = 0.40 ± 2 π ( 40 ) 2 2

∆ θ = 1600 π   r a d

Showww!

Passo 3

Bom, agora pra finalizarmos, a questão nos pediu o número de voltas, como uma volta vale 2 π   r a d , é só dividirmos ∆ θ por esse valor! Simbora:

1600 π r a d 2 π r a d = 800   v o l t a s    

Resposta

α = 2 π   r a d / s 2 e 800   v o l t a s

Exercícios de Livros Relacionados

O volante de uma máquina a vapor gira com uma velocidade angular constante de 150r e v / m i n . Quando a máquina é desligada, o atrito dos mancais e a resistência do ar param a roda em2,2h . (a) Qual
O prato de um toca-discos está girando a 33 1 3r e v / m i n . Uma semente de melancia está sobre o prato a 6,0c m de distância do eixo de rotação. (a) Calcule a aceleração da semente, supondo que ela
Na Figura 9.38 , o cilindro e a polia giram sem atrito em torno de um eixo horizontal fixo que passa pelos seus centros. Uma corda leve é enrolada em volta do cilindro, passa sobre a polia e possui um
Um roda começa a girar a partir do repouso em t= 0 com aceleração angular constante. No instante t=2,0s , a velocidade angular da roda é 5,0r a d / s . A aceleração cessa abruptamente no instante t=20
Um carro parte do repouso e se move em uma pista circular com 30,0m de raio . A velocidade do carro aumenta a uma taxa constante de 0 , 500m / s 2 . (a) Qual é o módulo da aceleração linear média do c