Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Oscilador Linear Massa-Mola

Ver Teoria
Exercício 2712345678910111213141516171819202122232425262829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586

Enunciado

Um bloco de massa m está conectado a uma mola de constante elástica k em um plano inclinado que forma um ângulo α em relação à horizontal. No instante t = 0 , o bloco é solto da posição x = 0 , com velocidade inicial nula. Considerando que a mola está relaxada (nem comprimida, nem esticada) quando x = 0 , determine:

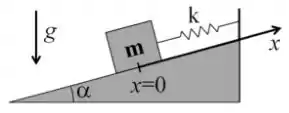
(a) A equação do movimento do bloco ao longo do eixo x mostrado na figura.

(b) A posição da massa x ( t ) em função do tempo. Qual é a amplitude do movimento e os valores máximo ( x m a x ) e mínimo ( x m i n ) de x ?

(c) A energia cinética em função do tempo.

Passo 1

(a) Precisamos aplicar a segunda lei de Newton aqui, fazendo o somatório de todas as forças que atuam no bloquinho: peso (P), normal (N) e força elástica ( F e l ) .

N → + P → + F e l → = m a →

Decompondo o peso, obtemos na direção x que

- m g s e n α - k x = m a

Como a = x ¨ , dividindo tudo por m e rearranjando

x ¨ + k m x = - g s e n ( α )

Que é uma EDO não-homogênea.

Passo 2

(b) A solução dessa EDO vai ter um termo homogêneo e um particular:

x t = x h + x p

Para a parte homogênea

x h ¨ + k m x h = 0

Cuja solução é oscilatória

x h t = A s e n ω t + B c o s ( ω t )

Onde

ω = k m

Para a solução particular, como a parte não-homogênea é constante, chutamos um valor constante.

x p = C

x p ¨ = 0

Jogando na EDO

0 + k m C = - g s e n α

C = - m g s e n α k

Juntando as soluções, obtemos

x t = - m g s e n α k + A s e n ω t + B c o s ( ω t )

Passo 3

Usando as condições iniciais para descobrir as constantes A e B .

x 0 = 0

x ˙ 0 = 0

x 0 = - m g s e n α k + B = 0

B = m g   s e n α k

Derivando x ( t )

x ˙ t = ω A c o s ω t - ω B s e n ( ω t )

x ˙ 0 = ω A = 0

A = 0

Assim, obtemos

x t = m g   s e n α k [ cos ⁡ ω t - 1 ]

Passo 4

Como o coseno   varia entre - 1 e 1 ,

x m i n = m g s e n α k - 1 - 1 = - 2 m g s e n α k

x m a x   = m g s e n α k 1 - 1 = 0

Passo 5

(c) A energia cinética é

K = m v 2 2

Onde a velocidade do bloco é dada por

v = x ˙ t = m g s e n α k ∙ d d t [ cos ⁡ ω t - 1 ]

v = - ω m g s e n α k s e n ( ω t )

K = m 2 ω m g s e n α k 2 s e n 2 ( ω t )

Resposta

(a) x ¨ + k m x = - g s e n ( α )

(b) x t = m g   s e n α k [ cos ⁡ ω t - 1 ]

x m i n = - 2 m g s e n α k

x m a x = 0

(c)

K = m 2 ω m g s e n α k 2 s e n 2 ( ω t )

Exercícios de Livros Relacionados

Na figura, um bloco pesando 14,0N , que pode deslizar sem atrito em um plano inclinado de ângulo θ = 40,0 ° , está ligado ao alto do plano inclinado por uma mola de massa desprezível de 0,450m de comp
Um oscilador é formado por um bloco preso a uma mola ( k = 400N / m ). Em um certo instante t , a posição (medida a partir da posição de equilíbrio do sistema), a velocidade e a aceleração do bloco sã
Um bloco de 1,2k g deslizando em uma superfície horizontal sem atrito está preso a uma mola horizontal com k = 480N / m . Seja x o deslocamento do bloco a partir da posição na qual a mola se encontra
A figura mostra uma massa de 1,0k g colocada sobre uma massa de 5,0k g que oscila sobre uma superfície sem atrito. A constante elástica é de 50N / m , e o coeficiente de atrito estático entre os dois
A figura mostra um bastão homogêneo de 200g com um orifício em uma das extremidades. A outra extremidade é presa a uma mola horizontal. Quando o bastão está suspenso exatamente na vertical, a mola não