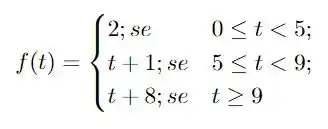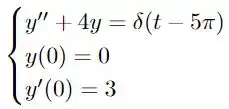Exercícios de Cálculo de Transformada de Laplace - Lista de Exercícios Resolvida
Questão 5
10. Suponha que exista para .
a) Mostre que se é uma constante positiva, então
Ver solução completaQuestão 6
Questão 1:
(b) Utilize a Transformada de Laplace para calcular a seguinte integral impropria.
Ver solução completaQuestão 13
10. Suponha que exista para .
(b) Mostre que se é uma constante positiva, então
Ver solução completaQuestão 14
Calcule a transformada de Laplace da seguinte função, indicando para que valores da variável a transformada é válida:
Questão 15
Questão 2: Faça o que se pede em cada item:
(B) Pela definição, calcule a transformada de Laplace da função (mostrando os passos):
Ver solução completaQuestão 16
Considere f(t) definida para . A Transformada de Laplace de é dada pela fórmula . Determine.
Ver solução completaQuestão 17
Sabendo que a Transformada de Laplace de uma função denotada aqui por é definida por:
Considere definida para . A de é dada pela fórmula
E usando a linearidade do operador em questão, determine a Transformada de Laplace da função elementar
Ver solução completaQuestão 18
Pela definição, calcule a transformada de Laplace da função (justificando os passos)
Ver solução completaQuestão 19
Determine a solução do problema de valor inicial utilizando a transformada de Laplace.
Ver solução completaQuestão 20
Determine a solução do problema de valor inicial utilizando a transformada de Laplace.
Ver solução completaQuestão 21
Determine a solução do problema de valor inicial utilizando a transformada de Laplace.
Ver solução completaQuestão 22
Determine a solução do problema de valor inicial utilizando a transformada de Laplace.
Ver solução completaQuestão 23
Determine a solução do problema de valor inicial utilizando a transformada de Laplace.
Ver solução completaQuestão 24
Determine a solução do problema de valor inicial utilizando a transformada de Laplace.
Ver solução completaQuestão 27
Seja . Qual das respostas abaixo representa a Transformada de Laplace da função ?
( )
( )
( )
( )
( )
Ver solução completaQuestão 28
Nos problemas de até , use a definição de transformada de Laplace para calcular
Ver solução completaQuestão 29
Nos problemas de até , use a tabela de transformada de Laplace para calcular
Ver solução completaQuestão 30
Nos problemas de até , use a definição de transformada de Laplace para calcular
Ver solução completaQuestão 32
Nos problemas de (a) até (j), use a tabela de transformada de Laplace para calcular .
(g)
Ver solução completaQuestão 33
Nos problemas de (a) até (j), use a tabela de transformada de Laplace para calcular .
(e)
Ver solução completaQuestão 34
Nos problemas de (a) até (j), use a tabela de transformada de Laplace para calcular .
(i)
Ver solução completaQuestão 35
Nos problemas de até , use a definição de transformada de Laplace para calcular
Ver solução completaQuestão 36
Nos problemas de até , use a tabela de transformada de Laplace para calcular
Ver solução completaQuestão 38
Nos problemas de (a) até (j), use a tabela de transformada de Laplace para calcular .
(g)
Ver solução completaQuestão 39
Nos problemas de (a) até (j), use a tabela de transformada de Laplace para calcular .
(i)
Ver solução completaQuestão 40
Nos problemas de (a) até (j), use a tabela de transformada de Laplace para calcular .
(f)
Ver solução completaQuestão 42
Nos problemas de até , use a definição de transformada de Laplace para calcular
Ver solução completaQuestão 43
Nos problemas de até , use a definição de transformada de Laplace para calcular
Ver solução completaQuestão 44
Nos problemas de até , use a definição de transformada de Laplace para calcular
Ver solução completaQuestão 45
Nos problemas de até , use a definição de transformada de Laplace para calcular
Ver solução completaQuestão 46
Nos problemas de até , use a definição de transformada de Laplace para calcular
Ver solução completaQuestão 47
Nos problemas de até , use a definição de transformada de Laplace para calcular
Ver solução completaQuestão 48
Considere definida para . A Transformada de Laplace de é dada pela fórmula
Determine .
Ver solução completaQuestão 49
Determine a Transformada de Laplace de e indique a única resposta correta:
Ver solução completaQuestão 51
Sabendo que a transformada de Laplace de uma função denotada aqui por é definida por
determine a transformada de Laplace da função elementar .
Ver solução completaQuestão 52
Determine a solução do problema de valor inicial utilizando a transformada de Laplace.
Ver solução completaQuestão 53
Utilizando o exercício anterior, para cada uma das funções especificadas a seguir, determine a função harmônica fora do círculo , que coincide com a função dada sobre a circunferência .
Ver solução completaQuestão 54
Utilizando o exercício anterior, para cada uma das funções especificadas a seguir, determine a função harmônica fora do círculo , que coincide com a função dada sobre a circunferência .
Ver solução completaQuestão 55
Utilizando o exercício anterior, para cada uma das funções especificadas a seguir, determine a função harmônica fora do círculo , que coincide com a função dada sobre a circunferência .
Ver solução completaQuestão 56
Verifique que todas as funções que sejam polinômios de e de primeira ordem satisfazem a equação de Laplace. (ou seja, são funções harmônicas).
Ver solução completaQuestão 57
Verifique que qualquer função de forma satisfaz a equação de Laplace. Aqui e são constantes arbitrárias.
Ver solução completaQuestão 58
Determine condições sobre as constantes e para que o polinômio homogêneo de segunda ordem satisfaça a equação de Laplace.
Ver solução completaQuestão 59
Sejam e funções harmônicas (i.e soluões da equação de Laplace).
Se é harmônica, prove que é harmônica, se e somente se, , para e constantes.
Ver solução completaQuestão 60
Escreva o problema de Dirichlet para a equação de Laplace satisfeito pela função no quadrado unitário
Ver solução completaQuestão 61
Sejam e funções harmônicas (i.e soluões da equação de Laplace).
Prove que também é uma função harmônica para quaisquer .
Ver solução completa