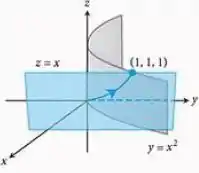
O campo é o campo de velocidades de um escoamento no espaço. Encontre o escoamento de até ao longo da curva de interseção do cilindro e do plano . (Sugestão: use como parâmetro.)
Passo 1
Na teoria a gente viu que escoamento nada mais é que a integral de linha:
O campo foi dado no enunciado , só fica faltando a parametrização da curva .
Então vamos começar por isso, né?
Passo 2
O exercício da uma dica boa de usar , então vamos usá-la. E isso dá que , certo?
Então, pelo cilindro, encontramos que a projeção no plano pode ser parametrizada por:
Mas aqui estamos no , então vamos usar a outra superfície para encontrar a parametrização da nossa curva no espaço.
E o que temos é algo simples, o plano , que nos dá também.
Assim temos que nossa curva tem parametrização:
Que vai de a , então , concorda?
Passo 3
Da parametrização podemos tirar o vetor tangente:
E agora já temos tudo que precisamos pra calcular a integral, é so jogar na fórmula!
Passo 4
Então, vamos ter que: