Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Vetorial no R³

Ver Teoria
Exercício 111234567891012131415161718192021222324252627282930313233343536373839

Enunciado

O campo de forças F → ( x , y , z ) = x - 2 , y - 2 , z - 4 x - 4 atua sobre uma partícula transladando-a ao longo da curva interseção das superfícies z = x 2 + y 2 e z = 4 x + 4 y - 4 , orientada de modo que sua projeção no plano x y seja percorrida uma vez, no sentido horário. Calcule o trabalho realizado por F →

Passo 1

Para acharmos o trabalho de F → devemos fazer a integral de linha de F → ao longo da curva C que é a interseção entre z = x 2 + y 2 e z = 4 x + 4 y - 4 :

T r a b a l h o = ∫ C   F → d r →

Encontrar uma solução para uma integral de linha nada mais é do que seguir um passo a passo maroto:

  1. Parametrizar a curva C que estamos trabalhando
  2. Substituir os termos do campo vetorial F → x ,   y pelos termos da parametrização
  3. Encontrar o termo d r →

Então vem comigo nessa aventura! :D

Passo 2

Vamos então parametrizar a curva C , mas por falar nisso, quem é a curva C ?

Como nos pediu o exercício, a curva é dado pela interseção do paraboloide de equação z = x 2 + y 2

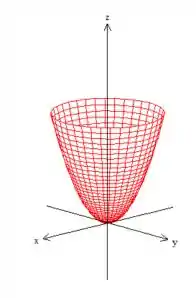
com esse plano z = 4 x + 4 y - 4 , bonitinho aqui:

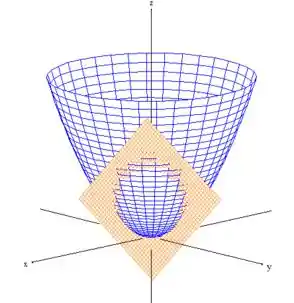
Sacou? :D

Passo 3

Pow, para achar essa intercessão aí na matemática, devemos realizar a interseção entre as duas superfícies, fazendo a igualdade entre elas

x 2 + y 2 = z = 4 x + 4 y - 4

Vamos ter

x 2 - 4 x + y 2 - 4 y = - 4

completando quadrados...

x 2 - 4 x + 4 + y 2 - 4 y + 4 = 4 + 4 - 4

x - 2 2 + y - 2 2 = 4

Isso é uma circunferência, vamos parametrizar essa circunferência:

x = 2 + 2 cos ⁡ θ

y = 2 + 2 sen ⁡ θ

Como ele quer rodar no sentido horário quando formos fazer a integral de linha vamos trocar o seu sinal no fim, isso porque a parametrização sendo assim a curva roda no sentido anti-horário.

Como temos uma circunferência toda na projeção no plano x y ...

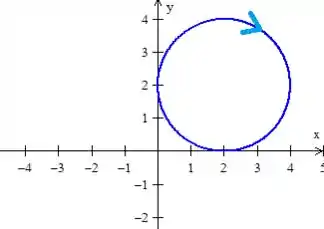
então θ da uma volta completa, o que significa

θ ∈ 0,2 π

Falta a componente z , mas temos uma relação entre z e y , x

z = 4 x + 4 y - 4

Então

z = 4 2 + 2 cos ⁡ θ + 4 2 + 2 sen ⁡ θ - 4

z = 8 + 8 cos ⁡ θ + 8 + 8 sen ⁡ θ - 4

z = 12 + 8 cos ⁡ θ + 8 sen ⁡ θ

Vamos ter no final, a parametrização:

σ θ = 2 + 2 cos ⁡ θ , 2 + 2 sen ⁡ θ , 12 + 8 cos ⁡ θ + 8 sen ⁡ θ

Com θ ∈ 0,2 π

Passo 4

Agora calculamos do d r → :

d r → = σ ' θ d θ

Derivando a parametrização:

σ ' t = ∂ ∂ θ 2 + 2 cos ⁡ θ , ∂ ∂ θ 2 + 2 sen ⁡ θ , ∂ ∂ θ 12 + 8 cos ⁡ θ + 8 sen ⁡ θ

σ ' t = - 2 sen ⁡ θ , 2 cos ⁡ θ , - 8 sen ⁡ θ + 8 cos ⁡ θ

Logo:

d r → = - 2 sen ⁡ θ , 2 cos ⁡ θ , - 8 sen ⁡ θ + 8 cos ⁡ θ d θ

Passo 5

Como vimos, precisamos colocar o sinal negativo na integral porque ele quer no sentido hor��rio e nossa orientação está no sentido anti-horário. Substituindo tudo...

- ∫ 0 2 π 2 + 2 cos ⁡ θ - 2 , 2 + 2 sen ⁡ θ - 2 , 12 + 8 cos ⁡ θ + 8 sen ⁡ θ - 4 2 + 2 cos ⁡ θ - 4 ∙ - 2 sen ⁡ θ , 2 cos ⁡ θ , - 8 sen ⁡ θ + 8 cos ⁡ θ d θ

= - ∫ 0 2 π 2 cos ⁡ θ , 2 sen ⁡ θ , 12 + 8 cos ⁡ θ + 8 sen ⁡ θ - 8 - 8 cos ⁡ θ - 4 ∙ - 2 sen ⁡ θ , 2 cos ⁡ θ , - 8 sen ⁡ θ + 8 cos ⁡ θ d θ

= - ∫ 0 2 π 2 cos ⁡ θ , 2 sen ⁡ θ , 8 sen ⁡ θ ∙ - 2 sen ⁡ θ , 2 cos ⁡ θ , - 8 sen ⁡ θ + 8 cos ⁡ θ d θ

= - ∫ 0 2 π - 4 sen ⁡ θ cos ⁡ θ + 4 sen ⁡ θ cos ⁡ θ - 64 sen 2 ⁡ θ + 64 cos ⁡ θ sen ⁡ θ d θ

= - ∫ 0 2 π - 64 sen 2 ⁡ θ + 64 cos ⁡ θ sen ⁡ θ d θ

= ∫ 0 2 π 64 sen 2 ⁡ θ - 64 cos ⁡ θ sen ⁡ θ d θ

Lembrando que

sen ⁡ θ cos ⁡ θ = sen ⁡ 2 θ 2

E

sen 2 ⁡ θ = 1 - cos ⁡ 2 θ 2

A integral vai ficar

= ∫ 0 2 π 64 1 - cos ⁡ 2 θ 2 - 64 sen ⁡ 2 θ 2 d θ

= ∫ 0 2 π 32 1 - cos ⁡ 2 θ - 32 sen ⁡ 2 θ d θ

= 32 ∫ 0 2 π 1 - cos ⁡ 2 θ - sen ⁡ 2 θ d θ

= 32 θ + sen ⁡ 2 θ 2 - cos ⁡ 2 θ 2 θ = 0 2 π

= 32 2 π + sen ⁡ 2 ∙ 2 π 2 - cos ⁡ 2 ∙ 2 π 2 - 0 + sen ⁡ 2 ∙ 0 2 - cos ⁡ 2 ∙ 0 2

= 32 2 π + sen ⁡ 4 π 2 - cos ⁡ 4 π 2 - 0 + sen ⁡ 0 2 - cos ⁡ 0 2

= 32 2 π + 0 - 1 - 0 + 0 - 1

= 32 2 π - 1 + 1

= 64 π

Resposta

64 π

Exercícios de Livros Relacionados

Nos exercícios 18 a 25, calcular as integrais curvilíneas dadas:24. ∫ C y d x + z d y - x y d z , onde C é dada por y = s e nx ; z = 4 ; x ∈ [ 0,2 π ] .
Nos exercícios 18 a 25, calcular as integrais curvilíneas dadas:22. ∫ C d x + d y + d z , onde C é a intersecção das superfícies y + z = 5 e z = 4 - x 2 do ponto A ( 2 ,5 ,0 ) ao ponto B ( - 2 ,5 ,0 )
Calcule ∫ γ d x + x y d y + zd z , onde γ é a interseção de x 2 + y 2 + z 2 = 2 ,x ≥ 0 ,y ≥ 0 e z ≥ 0 , com o plano y = x ; o sentido do percurso é do ponto 0,0 , 2 para 1,1 , 0 .
Calcule a integral de linha ∫ C F → ∙ d r → , onde C é dada pela função vetorial r → t . F → x ,y = x + yi ^ + y - z j ^ + z 2k ^ r → t = t 2i ^ + t 3j ^ + t 2k ^ , 0 ≤ t ≤ 1
Determine uma função f tal que F → = ∇ f e Use a parte (a) para calcular ∫ C F → ⋅ d r → sobre a curva C dada. F → x , y = y 2 c o s c o szi → + 2 x y c o szj → - x y 2 s e nz k → ,C : r → t = t 2 i →