Uma fenda com largura igual a é iluminada por um feixe de raios paralelos de comprimento de onda igual a .
A figura de difração é observada sobre uma tela situada a uma distância de da fenda.
A intensidade no centro do máximo central é igual a .
- Qual é a distância sobre a tela entre o centro do máximo central e o primeiro mínimo?
- Qual é a intensidade em um ponto situado no centro do segmento que une o máximo central com o primeiro mínimo?
Passo 1
O problema nos dá a largura da fenda , o comprimento de onda , a distância entre a fenda e a tela e a intensidade para .
a)
O problema nos pede para calcular a distância sobre a tela entre o centro do máximo central e o primeiro mínimo .
Essa distância é dada por:
Onde:
;
;
;
;
Logo:
Passo 2
b)
O problema nos pede para calcular a intensidade em um ponto situado no centro do segmento que une o máximo central com o primeiro mínimo.
Esse ponto se trata da metade da distância entre o máximo central e o primeiro mínimo, logo:
A intensidade é dada por:
Onde:
Como já possuímos os valores de e, nos falta apenas descobrir o valor de para resolver o problema.
Passo 3
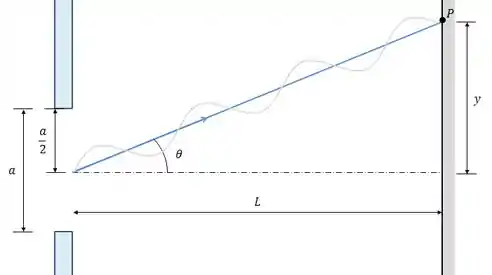
Analisando a figura abaixo, vemos que podemos encontrar o valor de através da seguinte relação:
Onde:
;
;
Logo:
Como então:
Passo 4
Onde:
;
;
;
Logo:
Passo 5
Onde:
;
;
;
Logo:
Resposta
a)
b)