Física 4 – UFRJ – 2019.1 – PF – Questão 9
A luz de um laser de He-Ne de comprimento de onda de incide numa fenda simples com largura de . Qual é o comprimento do máximo central (a distância entre franjas escuras contíguas ao máximo central) num anteparo a de distância?
a) .
b) .
c) .
d) .
Passo 1
Fala pessoal, beleza?
Nesse problema vamos brincar um pouco com difração por uma fenda simples. Sabemos que nesse caso, a intensidade é dada por
Nessa expressão, é o tamanho da fenda. No desenho a seguir temos o esquema da situação:
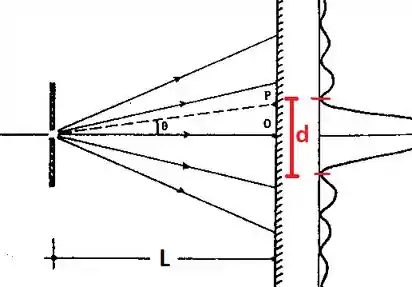
Nosso objetivo é achar que representa a distância entre os mínimos que delimitam o máximo central.
Para achar as franjas escuras (pontos de mínimo), temos que zerar a intensidade:
Vale ressaltar que não vale, pois nesse caso temos uma indeterminação do tipo que dá . Na verdade, esse ponto corresponde ao máximo central. Os pontos pintados em vermelho na figura correspondem a e .
Passo 2
Usando a expressão de :
Usando a aproximação de ângulos pequenos:
Logo,
Para , temos que
Já para ,
O tamanho do máximo central é dado por
Daí é só substituir:
Assim,
Com isso, podemos assinalar a alternativa A!
Resposta
Alternativa A.