Uma luz monocromática com um comprimento de onda de incide em uma fenda com de largura. A distância entre a fenda e a tela é .
Considere um ponto da tela situado a de distância do máximo central. Calcule:
- O valor de nesse ponto.
- O valor de .
- A razão entre a intensidade nesse ponto e a intensidade do máximo central.
Passo 1
a)
O ângulo entre a reta que vai da fenda até o máximo central da figura de difração e a reta que vai até o ponto que queremos avaliar é .
Se olharmos essas duas retas e a distância desse ponto até o máximo central, nós temos um triângulo retângulo onde os catetos são a distância até o anteparo e a distância do ponto ao máximo central .
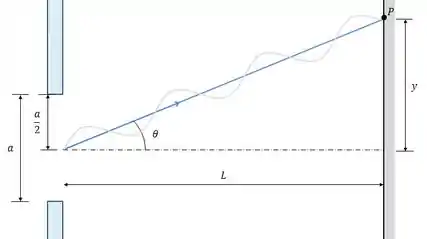
A tangente de será então:
Passo 2
b)
é a diferença de fase entre todos os raios que atingem o ponto que estamos analisando. Ela vai ser dada por:
A fenda tem uma largura de e a luz que incidente tem comprimento de onda . Substituindo esses valores junto com o ângulo encontrado no item anterior, ficamos com:
Passo 3
c)
A intensidade nesse ponto é dada por:
A razão entre essa intensidade e o máximo central vai ser
Resposta
a)
b)
c)