Luz proveniente de uma fonte monocromática de comprimento de onda é difratada por uma fenda de largura em um anteparo paralelo às frentes de ondas planas. A figura de difração é observada em uma tela distante.
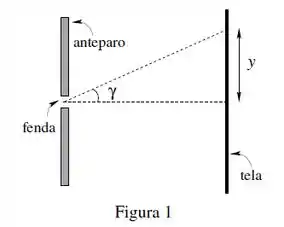
(a) Se o primeiro mínimo da figura de difração ocorre em um determinado ângulo contado a partir da região central, calcule a largura da fenda. Considere a aproximação válida para ângulos pequenos.
(b) Num segundo experimento, luz de comprimento de onda é difratada pela mesma fenda produzindo o primeiro máximo secundário no mesmo ângulo do item (a). Qual a relação entre e ?
(c) Calcule a abertura da fenda para que a largura da franja brilhante na região central da figura de difração seja diminuída para 1/3 do valor.
Passo 1
(a) Sabemos que os pontos de mínimo da figura de difração produzidos por uma fenda de largura são dados pela fórmula:
onde
Então o primeiro mínimo da figura de difração é dado por:
Usando a aproximação para ângulos pequenos :
Logo:
Passo 2
(b) Agora a gente tem uma outra luz, com comprimento de onda , que tem o seu primeiro máximo secundário no mesmo ângulo que tínhamos no item (a).
Tínhamos achado que:
Logo:
A gente não sabe calcular a posição de um máximo secundário!!
Mas sabemos que entre dois mínimos, existe um máximo secundário.
Vamos considerar então que esse máximo esteja no meio dos dois mínimos adjacentes, que são e
Vamos começar calculando as posições (ângulos) desses mínimos.
Para
Já para
O ângulo médio entre esses dois caras é:
Igualando com o que tínhamos antes:
Passo 3
(c) Vamos usar um raciocínio parecido com o do item anterior.
De novo a gente não sabe calcular a posição do máximo central.
Mas sabemos que ele tá entre o mínimo de posição e
Ou seja, vai ser o dobro do ângulo que a gente achar para pois vamos ter esse ângulo para cima do máximo central e para baixo.
Então:
Como foi pedido no enunciado, queremos que:
Se mantemos o mesmo comprimento de onda e só mudamos a largura da fenda, vamos ter:
Resposta
(a)
(b)
(c)