Exercícios de Efeito Fotoelétrico - Lista de Exercícios Resolvida
Questão 1
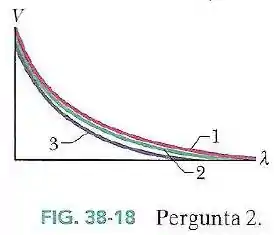
A Fig.38-18 mostra a tensão de corte em função do comprimento de onda da luz para três materiais diferentes.
Coloque os materiais na ordem da função trabalho, começando pela maior.
Questão 2
A função trabalho do Césio é . Qual a energia cinética máxima dos elétrons emitidos, em , se o comprimento de onda da radiação incidente for igual a ?
- Nenhuma das anteriores
Questão 3
O potencial de corte para elétrons emitidos de uma superfície iluminada por uma luz com um comprimento de onda de é .
Quando o comprimento de onda da luz incidente é mudado para um novo valor, o potencial de corte muda para .
- Qual é o valor do novo comprimento de onda?
- Qual é a função trabalho da superfície?
Questão 4
Uma placa de alumínio é iluminada por luz com um comprimento de onda de .
No alumínio uma energia de é necessária para que um elétron seja ejetado.
Qual é o potencial de corte?
Ver solução completaQuestão 5
O comprimento de onda correspondente à frequência de corte da prata é .
Determine a energia cinética máxima dos elétrons ejetados de uma placa de prata iluminada por luz ultravioleta com um comprimento de onda de .
Ver solução completaQuestão 6
O leitor precisa escolher um elemento para uma célula fotoelétrica que funcione com luz visível. Quais dos seguintes elementos são apropriados (a função trabalho aparece entre parênteses)?
- Tântalo ()
- Tungstênio ()
- Alumínio ()
- Bário ()
- Lítio ()
Obs: O comprimento de onda da luz visível varia aproximadamente de até .
Ver solução completaQuestão 7
- Para ejetar um elétron do sódio é preciso uma energia de pelo menos . O efeito fotoelétrico é observado quando uma placa de sódio é iluminada com luz vermelha de comprimento de onda ?
- Qual é o comprimento de onda de corte para a emissão fotoelétrica no caso do sódio?
Ver solução completaQuestão 8
Para um material fotoelétrico foi medido o potencial de corte em função da frequência da luz incidente e o resultado está na figura anexa.
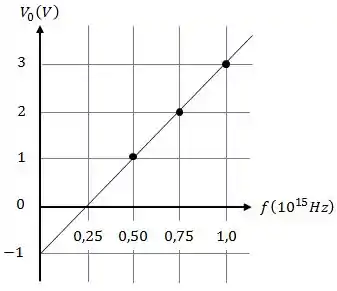
O valor da função trabalho para este material é:
Não pode ser calculado apenas com os dados fornecidos
Nenhuma das anteriores
Ver solução completaQuestão 9
A eficiência relativa de uma superfície de césio (cuja função trabalho é ) é , isto é, em média um elétron é ejetado para cada fótons que incidem na superfície.
Qual é a corrente elétrica produzida pelos elétrons ejetados de uma placa de césio iluminada pela luz de produzida por um laser de ?
Suponha que todos os elétrons ejetados contribuem para a corrente.
Obs: A carga elementar do elétron é de
Ver solução completaQuestão 10
Uma placa de alumínio é iluminada por luz com um comprimento de onda de .
No alumínio uma energia de é necessária para que um elétron seja ejetado.
Qual é a energia cinética:
- Do elétron ejetado mais rápido?
- Do elétron ejetado mais lento?
- Qual é o comprimento de onda de corte do alumínio?
Questão 11
A função trabalho do Césio é . Qual a energia cinética máxima dos elétrons emitidos, em , se o comprimento de onda da radiação incidente for igual a ?
- Nenhuma das anteriores
Questão 12
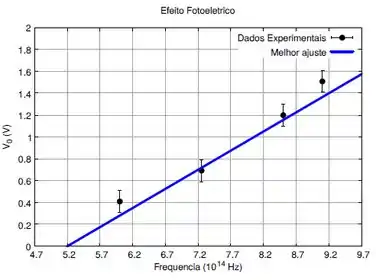
Um estudante de laboratório de Física Moderna realiza um experimento para estimar a constante de Planck e a função trabalho de um material, observando o efeito fotoelétrico.
Os pontos experimentais obtidos do potencial de freamento versus a frequência da luz incidente para um mesmo material estão no gráfico a seguir. A curva contínua representa a reta que melhor se ajusta aos dados experimentais.
Baseando-se apenas no gráfico e desconsiderando as incertezas, a constante de Planck é estimada pelo valor:
Questão 13
Para um material fotoelétrico foi medido o potencial de corte em função da frequência da luz incidente e o resultado está na figura anexa.
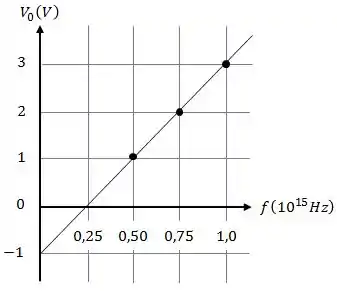
O valor da função trabalho para este material é:
Não pode ser calculado apenas com os dados fornecidos
Nenhuma das anteriores
Ver solução completaQuestão 14
Em um experimento do efeito fotoelétrico foi encontrado o potencial de corte em função dos comprimentos de onda no lítio, como representado na figura
A partir da informação contida na figura, determine:
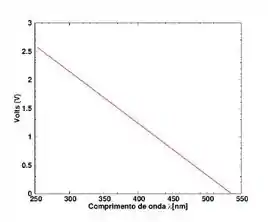
a) O valor da constante de Planck
b) A função de trabalho do lítio (em eV)
Ver solução completaQuestão 15
A função de trabalho para o metal lantânio é de . Suponha que uma placa deste metal seja iluminada com luz de comprimento de onda igual a .
Considere os fotoelétrons não relativísticos emitidos da placa com o máximo de energia possível. Nessas condições
- Calcule o valor da energia cinética desses elétrons.
- Calcule o comprimento de onda de de Broglie desses elétrons. Dê sua resposta em função da constante de Planck , da massa do elétron e de sua energia cinética .
Questão 16
Em um experimento de efeito fotoelétrico, observou-se que os elétrons são arrancados do cátodo apenas com radiação de comprimento de onda menor que . Com base nisso, podemos afirmar que a função trabalho do cátodo é
a).
b) .
c) .
d) .
Ver solução completaQuestão 17
Numa aula de física moderna, um estudante obtém os seguintes valores para o potencial de corte, e , para as frequências de luz incidente e , respectivamente. Com esses dados, a razão entre a carga do elétron pela constante de Planck, , pode ser dada pela expressão:
a) .
b) .
c) .
d) .
e) Impossível encontrar esta quantidade.
Ver solução completaQuestão 18
Um laser de Argônio, com comprimento de onda de , potência de e diâmetro do feixe de , atinge uma superfície de Césio, cuja função trabalho é de ;
a) De acordo com a teoria quântica para a radiação, quantos fótons por segundo o feixe do laser fornece?
b) De acordo com a teoria clássica da luz, e tomando a área da seção reta do Césio como a de absorção da luz, calcule o tempo mínimo que levaria para um elétron ser emitido.
(Dado: raio do Césio é .)
c) Qual é o potencial de frenagem para os elétrons emitidos?
d) Qual é a frequência de corte do Césio?
e) Por que a existência de uma frequência de corte é evidência da Teoria de Einstein para o efeito fotoelétrico?
Ver solução completaQuestão 19
Um estudante de laboratório de Física Moderna realiza um experimento para estimar a constante de Planck e a função trabalho de um material, observando o efeito fotoelétrico. Os pontos experimentais obtidos do potencial de corte versus a frequência da luz incidente para um mesmo material estão no gráfico a seguir. A curva contínua representa uma porção da reta que melhor se ajusta aos dados experimentais.
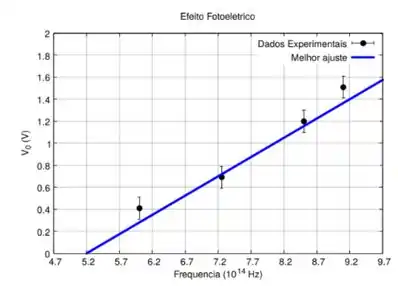
Através do gráfico, determine a função trabalho do material:
a) .
b) .
c) .
d) .
Ver solução completaQuestão 20
Um material é iluminado com luz de frequência , obtendo-se o valor do potencial de corte de .
O valor da frequência de corte da luz, para o qual o efeito fotoelétrico cessa, é dado aproximadamente por
Questão 21
Um material é iluminado com luz de dois comprimentos de onda e , com potenciais de freamento e , respectivamente.
A função trabalho deste material é dada por
Questão 22
Em uma experiência de efeito fotoelétrico, uma superfície metálica é bombardeada por fótons com energia de , e a energia cinética máxima dos fotoelétrons observada é .
Qual é a energia máxima dos fotoelétrons quando se dobra o comprimento de onda dos fótons incidentes?
Questão 23
No Potássio (K) o comprimento de onda acima do qual não existe o efeito fotoelétrico é
𝜆 = 558 𝑛𝑚.
(b) Obtenha a função trabalho do Potássio
(c) Calcule o potencial de frenagem no Potássio para uma radiação incidente de comprimento de onda 450 𝑛𝑚
Ver solução completaQuestão 24
Produz-se o efeito fotoelétrico no revestimento de Níquel sobre outro material com ondas EM de comprimento de onda 100 𝑛𝑚. A função trabalho desse metal tem valor 5,01 𝑒𝑉. Encontre o potencial de frenagem para esse comprimento de onda.
Ver solução completaQuestão 25
No Potássio (K) o comprimento de onda acima do qual não existe o efeito fotoelétrico é
𝜆 = 558 𝑛𝑚.
(b) Obtenha a função trabalho do Potássio.
(c) Calcule o potencial de frenagemno Potássio para uma radiação incidente de comprimento de onda 400 𝑛𝑚.
Ver solução completaQuestão 26
Considere os seguintes elementos com suas respectivas funções-trabalho aproximadas: Potássio (), Sódio (), Magnésio () e Prata (). Suponha que se faça incidir luz sobre cada um desses elementos com comprimentos de onda que variam de até . Em quais dos elementos listados anteriormente a luz incidente é capaz de arrancar elétrons do material?
a) Somente no Potássio e no Sódio.
b) Somente no Potássio.
c) Em todos eles, exceto na Prata.
d) Em nenhum deles.
e) Em todos eles, sem exceção.
Ver solução completaQuestão 27
Num experimento fotoelétrico realizado com ouro, cuja função-trabalho vale , utiliza-se radiação eletromagnética com comprimento de onda de . A energia cinética máxima dos elétrons arrancados vale:
a) .
b) .
c) .
d) .
e) .
Ver solução completaQuestão 28
A função-trabalho do ouro vale, aproximadamente, . Para se ter o efeito fotoelétrico com ouro, o comprimento de onda de uma onda eletromagnética deve ser menor que:
a) .
b) .
c) .
d) .
e) .
Ver solução completaQuestão 29
Numa célula fotoelétrica, luz de comprimento de onda e intensidade incide normalmente sobre o catodo de área A e função trabalho
(a) Qual é a máxima velocidade dos elétrons de massa m removidos do material? Despreze os efeitos relativísticos.
(b) Calcule o número N de fótons por segundo que atingem o catodo.
(c) Sabendo que apenas 5% dos fótons incidentes são absorvidos pelos elétrons (com carga determine a corrente fotoelétrica.
Ver solução completaQuestão 30
Em um experimento para testar o efeito fotoelétrico, usando um material cuja função trabalho é de , verifica-se que a diferença de potencial entre o anodo e o catodo deve ser de para que a corrente elétrica seja nula. Qual é o momento linear dos fótons que iluminam o material?
Questão 31
Uma placa de ouro é iluminada por uma luz de comprimento de onda de e elétrons são ejetados. A função trabalho para o ouro é de .
Qual é a energia cinética do elétron mais rápido?
Qual o comprimento de onda de corte para o efeito fotoelétrico ocorrer com o ouro como material?
Ver solução completaQuestão 32
A função trabalho do tungstênio é . Uma superfície desse metal é iluminada com luz de .
Determine o comprimento de onda dessa luz e a frequência de corte desse metal.
Calcue a energia cinética máxima , em Joules, dos elétrons ejetados.
Obtenha a energia total desses elétrons
Ver solução completaQuestão 33
Uma superfície metálica iluminada por uma luz de frequência igual a emite elétrons com energia cinética máxima igual a .
A mesma superfície é iluminada por uma luz de frequência igual a . Nesse caso, a energia cinética máxima dos fotoelétrons vale .
Com esses dados, calcule:
A constante de Planck .
A função trabalho do material.
Ver solução completaQuestão 34
Considere uma célula fotoelétrica de tungstênio, cuja função trabalho é igual a .
Se a radiação incidente sobre esta célula tiver uma frequência igual a , podemos afirmar que:
- Os elétrons ejetados terão uma energia de
- Os elétrons ejetados terão uma energia de
- Os elétrons ejetados terão uma energia de
- Os elétrons ejetados terão uma energia de
- Nenhum elétron será ejetado
- Nenhuma das respostas anteriores
Questão 35
Suponha que um satélite seja revestido de platina, cuja função trabalho vale . Ele é iluminado com fótons de energia .
Determine o comprimento de onda dessa onda EM e o comprimento de onda máximo de radiação incidente capaz de ejetar elétrons da superfícies do satélite.
Calcule a energia cinética máxima dos elétrons ejetados.
Obtenha a energia total desses elétrons
Ver solução completaQuestão 36
Luz incide sobre uma placa fotográfica e será “gravada” se dissociar uma molécula de da placa.
A energia mínima para dissociar essa molécula é da ordem de . Qual é a região de comprimentos de onda de luz que pode ser gravada nessa placa?
Ver solução completaQuestão 37
Um estudante de laboratório de Física Moderna realiza um experimento para estimar a constante de Planck e a função trabalho de um material, observando o efeito fotoelétrico.
Os pontos experimentais obtidos do potencial de freamento versus a frequência da luz incidente estão no gráfico a seguir. A curva contínua representa a reta que melhor se ajusta aos dados experimentais.
Baseando-se apenas no gráfico, a função trabalho do material é estimada pelo valor:
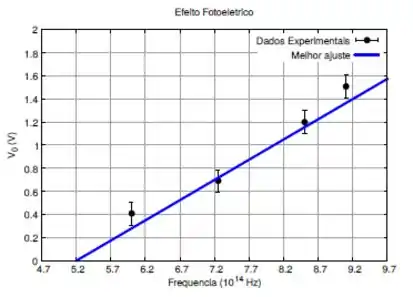
Questão 38
O efeito fotoelétrico ocorre a partir de um dado valor mínimo para a freqüência de oscilação da radiação eletromagnética, a qual ilumina um dado material condutor que compõe o experimento. Para um dado material, observa-se que com uma radiação com de comprimento de onda, o potencial de corte é . Para o efeito fotoelétrico ocorrer com esse material, é necessário que a freqüência da radiação utilizada seja maior que o valor:
Escolha uma:
Questão 39
Luz monocromática de comprimento de onda e de intensidade incide perpendicularmente sobre uma superfície metálica de área .
- Quantos fótons por segundo incidem sobre a superfície metálica?
- Calcule em a função de trabalho do metal sabendo que os elétrons mais energéticos arrancados do metal têm energia cinética igual a .
Questão 40
A função trabalho de um metal é . Calcule o maior comprimento de onda da radiação que ao incidir sobre esse metal ejeta elétrons da sua superfície. Considere h e c dados.
Ver solução completaQuestão 41
Um feixe de luz de comprimento de onda λ e intensidade I, incide sobre uma placa de área A, no interior de uma célula fotoelétrica. O material da placa possui função trabalho .
(a) Calcule e energia e o módulo do momento dos fótons incidentes.
(b) Calcule o número N de fótons incidentes sobre a placa em um intervalo de tempo ∆t.
(c) Determine a condição que deve ser satisfeita pelo valor de λ para que sejam ejetados elétrons do material.
Ver solução completaQuestão 42
Faça a escolha correta e justifique: Quanto ao Efeito Fotoelétrico, é INCORRETO afirmar:
(a) Existe uma frequência de corte abaixo da qual não há o efeito.
(b) O potencial de frenagem (de corte) é o mesmo para intensidades diferentes da radiação incidente no material com a mesma frequência (acima da frequência de corte).
(c) O potencial de frenagem ocorre quando a energia da radiação incidente não é superior à função trabalho do material.
(d) O potencial de corte corresponde à energia cinética máxima dos elétrons ejetados.
Ver solução completaQuestão 43
Luz monocromática de comprimento de onda , proveniente de uma fonte com intensidade , incide sobre três superfícies metálicas constituídas de lítio (Li), berílio (Be) e mercúrio (Hg). As funções de trabalho de cada um destes materiais são dadas por , e , respectivamente.
(a) Determine em que casos é possível observar o efeito fotoelétrico.
(b) Calcule a diferença de potencial necessária para frear os fotoelétrons (potencial frenador ou potencial de corte) nos casos em que os fotoelétrons são observados, conforme o item (a)
(c) Se ao invés da fonte com intensidade tivéssemos utilizado uma fonte com intensidade , mas com o mesmo comprimento de onda , como mudariam os itens (a) e (b) e o número de fotoelétrons emitidos?
Ver solução completaQuestão 44
Considere as seguintes afirmações:
- A relação entre a energia total e momento linear para um fóton pode ser obtida da relação relativística, tomando a massa de repouso do fóton infinita.
- Duas partículas com o mesmo momento linear e mesma energia total relativística possuem, necessariamente, a mesma massa de repouso.
- Um elétron em repouso emite um fóton e, por isso, sua massa de repouso é diminuída.
- Apenas é verdadeira.
- Apenas é verdadeira.
- Apenas é verdadeira.
- Apenas e são verdadeiras.
- Apenas e são verdadeiras.
- Apenas e são verdadeiras.
- Todas as afirmativas são verdadeiras.
- Nenhuma afirmativa é verdadeira.
Questão 45
Em uma experiência sobre efeito fotoelétrico, obtiveram curvas de corrente como função da diferença de potencial para dois conjuntos de feixes luminosos e potências e . Assuma o valor para a constante de Planck.
a) Qual é a energia dos fótons, em , para cada feixe?
b) Obtenha a função trabalho do metal (em ) considerando que o potencial de freiamento dos elétrons do feixe (1) é igual a . Em seguida obtenha o potencial de freiamente para os elétrons do feixe (2).
c) Quantos elétrons (por segundo) o feixe de menor potência consegue arrancar do metal, sabendo-se que a probabilidade de um elétron ser arrancado por um fóton desse feixe é ?
Ver solução completaQuestão 46
Uma lâmpada de luz ultravioleta é coberta com um filtro que permite apenas a passagem de luz de comprimento de onda igual a .
Quando a luz transmitida incide sobre uma superfície metálica, observa-se um fluxo de elétrons emergindo do metal.
- Se a intensidade da luz que atinge a superfície é dobrada,
- mais elétrons são emitidos por unidade de tempo.
- os elétrons emitidos têm maior energia.
- as afirmativas e são falsas.
- as afirmativas e são verdadeiras.
- O filtro é substituído por outro que transmite apenas luz com comprimento de onda de e a lâmpada é ajustada para que a intensidade luminosa incidindo sobre a superfície permaneça a mesma que para luz de comprimento de onda de .
Justifique sua resposta. Não basta indicar a alternativa correta.
Com a luz de comprimento de onda de ,
- mais elétrons são emitidos por unidade de tempo.
- os elétrons emitidos têm maior energia.
- as afirmativas e são falsas.
- as afirmativas e são verdadeiras.
Justifique sua resposta. Não basta indicar a alternativa correta.
Ver solução completaQuestão 47
Uma superfície de prata é irradiada com luz ultravioleta de comprimento de onda . Nestas condições, elétrons são liberados da superfície e, para freá-los completamente, é necessária uma d.d.p de .
a) Qual é a função trabalho deste material?
b) Qual é o maior comprimento de onda para o qual o é possível a emissão de elétrons da superfície?
Suponha agora que a superfície é irradiada com raios-X de comprimento de onda .
c) Qual é a energia de um fóton espalhado a em relação à direção do feixe de incidência, após a colisão com um elétron da superfície?
d) Encontre a direção e o módulo do momento do elétron espalhado, na condição do item (c).
e) BÔNUS – O elétron sai com velocidade relativística? Justifique!
Ver solução completaQuestão 48
A superfície de um metal que apresenta efeito fotoelétrico é iluminada com luz monocromática de comprimento de onda ajustável . Quando , o potencial de corte dos fotoelétrons é . Quando , o potencial de corte dos fotoelétrons é .
Usando estes dados, a carga do elétron e a velocidade da luz calcule a constante de Planck .
Ver solução completa