UFF, Cálculo IA-Lista 1, GMA, 2008-1, 44
Esboce o gráfico da função, especificando o domínio, a imagem e, quando possível, a paridade (par ou ímpar).
Passo 1
A única restrição da função é o denominador que não pode zerar:
Então o domínio é .
Passo 2
Vamos primeiro dar uma melhorada nesse polinômio aí do numerador, porque trabalhar com grau 3 não é muito bacana.
Agora é lembrar aqueles macetes que vimos pra procurar raízes de polinômios. No caso temos:
Queremos raízes na forma , sendo que (o coeficiente que multiplica ) é divisível por e é divisível por .
Ou seja, e .
Assim, as potenciais raízes são .
Passo 3
Então vamos testar... A boa é começar pelos números menores que vão dar menos conta.
:
:
Opa, então é uma raiz!
:
Mais uma raiz!
:
:
Show, achamos a última raiz, já podemos parar por aqui. Concluímos que
Passo 4
Mas na expressão da função aparece o módulo desse polinômio, então vamos ter que estudar o sinal dele. Os intervalos de interesse vão ser e .
Então vamos lá!
:
:
:
:
Passo 5
Ou seja, temos nos intervalos e .
Por outro lado, nos intervalos e .
E ainda temos que:
(Isso com , que já é uma condição do nosso domínio.)
Passo 6
A partir disso tudo podemos definir a expressão da função sem módulo:
Eita função indecisa, não para de mudar de sinal...!
Para e ela é voltada pra baixo:
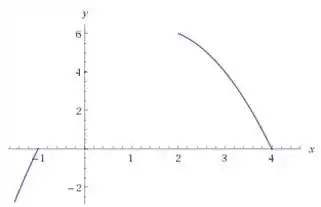
Para e ela é voltada pra cima:
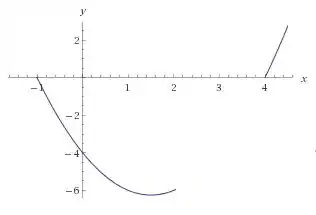
Passo 7
Juntando os dois, obtemos finalmente o gráfico desejado:
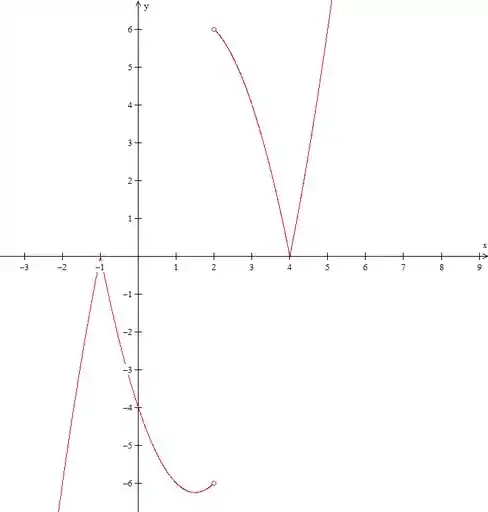
Repare que a imagem da função é todo o , e que ela não é nem par nem ímpar.
Resposta
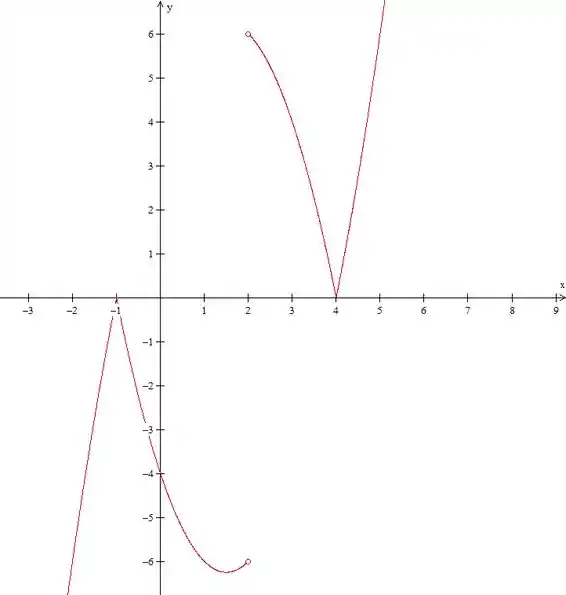
Não é par nem ímpar