Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Função Modular

Ver Teoria
Exercício 4123567891011121314151617181920212223242526272829

Enunciado

Seja f x = x 2 2 - 2 .

a) Para quais valores reais de x temos f x = 1 ?

b) Para quais valores reais de x temos f x ≤ 1 ?

Passo 1

Lá vamos nós para a letra a), para resolvermos essa parada aí, vamos igualar a nossa função a 1. Daí, teremos o seguinte:

x 2 2 - 2 = 1

Ou seja,

x 2 2 - 2 = 1           o u         x 2 2 - 2 = - 1

Vamos resolver essas duas equações agora, a primeira vai ficar assim:

x 2 2 - 2 = 1  

x 2 2 = 3        

x ² = 6          

x = ± 6

Agora, vamos para a segunda:

x 2 2 - 2 = - 1  

x 2 2 = 1        

x ² = 2          

x = ± 2

Tranquilinho, né?

Passo 2

#Partiu letra b) agora hein ...

Para descobrirmos onde a nossa função tem valores menores ou iguais a 1, vamos observar o gráfico dela.

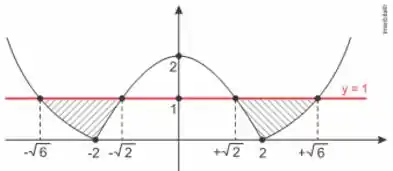
Perceba que a função tem y menor ou iguais a 1 para os seguintes valores:

- 6 ≤ x ≤ - 2       o u     2 ≤ x ≤ 6      

Resposta

a)   x = ± 6 ou x = ± 2

b)   - 6 ≤ x ≤ - 2       o u     2 ≤ x ≤ 6

Exercícios de Livros Relacionados

Encontre o domínio e esboce o gráfico da função: F x = 2 x + 1
Encontre o domínio e esboce o gráfico da função: g x = x x 2
1.45. Encontre o domínio e esboce o gráfico da função. G x = 3 x + | x | x
Esboce o gráfico:f (x) = |x + 1| - |x|
Esboce o gráfico:f (x) = ||x| - 1|