UFF, Cálculo IA-Lista 2, GMA, 2008-1, Questão 17
Esboce o gráfico da função
Passo 1
Perceba que não existem valores de que tornem essa função inexistente, logo não teremos preocupações quanto ao domínio.
Passo 2
Vamos começar a fazer o esboço. Olhando pra função dada, a função mais genérica que parece com ela é:
Construiremos nosso gráfico a partir do gráfico dessa função, que é simples de esboçar, pois trata-se de uma parábola com concavidade para cima e raízes e . E ele fica assim:
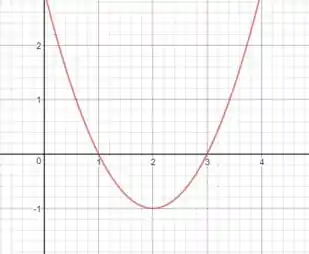
Passo 3
A primeira alteração feita na função acima é a colocação do módulo em . Se sacarmos que , então:
O módulo no faz com que seja sempre negativo, independentemente do valor de . No que isso implica? O gráfico no lado esquerdo do eixo será idêntico ao gráfico no lado direito desse eixo. Portanto, teremos que espelhar o gráfico em torno do eixo .
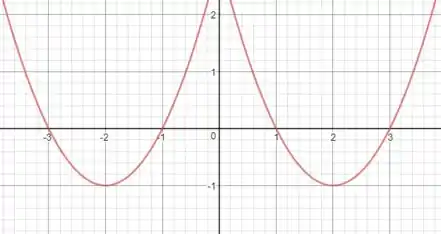
Passo 4
Passo 5
Passo 6
Finalmente, só resta aplicar o módulo em toda a função.
Essa operação transforma todos os valores negativos em positivos, portanto as partes do gráfico que estão abaixo do eixo serão rotacionadas para cima do eixo .
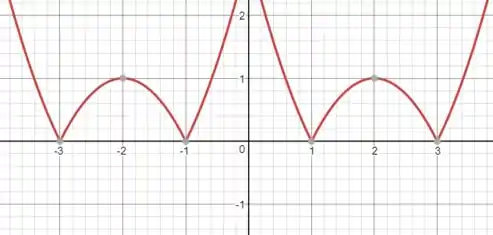
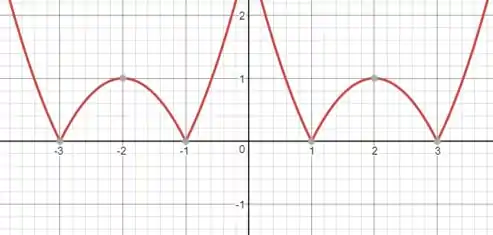
Resposta
