Calcular o valor de para que as retas
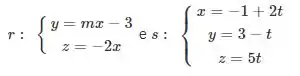
Sejam ortogonais.
Passo 1
Esse exercício também quer saber o valor de .
Devemos achar , mas agora para que as retas sejam ORTOGONAIS. Para que elas sejam ortogonais o produto interno entre os vetores diretores das retas deve ser ZERO, então:
Passo 2
Primeiro, vamos retirar das equações que nos foram dadas o vetor diretor de cada reta. Para retirar o vetor diretor da reta será um pouco mais chatinho, pois ela está no formato reduzido. Mas, não se desespere!! Vamos, com calma!!
Como ela está no formato reduzido, sabemos que um ponto genérico da reta pode ser escrito da seguinte forma:
Como para determinar um vetor precisamos de dois pontos, então escolhemos dois pontos aleatórios:
Sabendo que esses dois pontos pertencem à reta , podemos encontrar o vetor diretor da reta:
O vetor diretor da reta é mais fácil saber, pois temos as equações paramétricas da reta, então o vetor diretor fica explícito na equação:
Passo 3
Agora que já sabemos os vetores diretores é só fazer o produto interno e forçar para que ele dê ZERO para que sejam ortogonais as retas.
Portanto, para as retas serem ortogonais . Logo, o vetor diretor da reta r será: