UNB – Sem campus - Introdução a Álgebra Linear – Listas – Listas de IAL UnB – Lista 2 – 3a
Encontre os valores de para os quais .
Passo 1
Opa meus lindos, tudo bem com vocês? Bora lá resolver essa questão! Aqui somos apresentados pra matriz:
Uma matriz um pouco “estranha” por que a gente tem essas variáveis , mas tudo nos conformes. E dela, temos que achar os valores que pode assumir para que o determinante da matriz seja igual a 0. Showzinho, então temos que começar calculando o determinante e tornando ele igual a 0. Você manja de como podemos calcular o determinante dessa matriz? Relaxa que eu te mostro.
Passo 2
Show, temos uma matriz 2X2. Pra o determinante dela, o método mais tranquilo é a gente fazer o produto dos elementos da diagonal principal subtraídos do produto dos elementos da diagonal secundária. Ou seja:
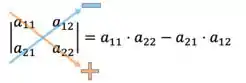
Pra nossa matriz, temos então:
Show, conseguimos achar o determinante.
Passo 3
Belezinha, determinante encontrado. Agora, vamos adotar a condição que a questão impôs. Ou seja, o determinante ser igual a 0. Dessa forma temos:
Olha só, um polinômio! E ele tem diversas raízes, ou diversas soluções, pra isso ser igual a 0. Essas soluções são justamente os valores de que queremos. Aqui, basta a gente calcular pelo método de Bhaskara. Portanto, calculando o
Calculando as raízes:
Dessa forma, as raízes pra esse polinômio, são:
Portanto, esses são os valores que pode assumir para que o determinante da nossa matriz seja 0! E é isso gente boa! Se ficou alguma dúvida, quer dar alguma sugestão ou reportar algum erro, manda um feedback pra gente! Vamos adorar ajudar você