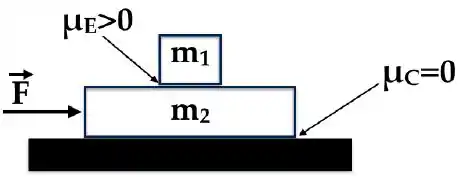
Dois blocos escorregam juntos sobre uma superfície horizontal sem atrito. O bloco de cima tem massa e de baixo e o atrito entre elas tem um coeficiente estático . Uma força horizontal de módulo atua sobre o bloco de baixo. Qual é a condição sobre para que os dois blocos não deslizam entre si?
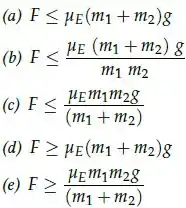
Passo 1
Para eles não deslizarem entre si, eles tem que ter a mesma aceleração certo? Se tivessem aceleração diferentes, eles iriam percorrer distância diferente e não iam ficar juntos!
Se a gente seperar os blocos vamos perceber que as forças que atuam no bloco são essas aqui ó:
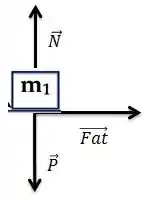
Então essa força de atrito vai ser a força que vai acelerar o bloco na horizontal !! Sendo assim, precisamos calcular quando essa força é máxima, que é justamente quanto o atrito é máximo.
E agora vamos calcular a aceleração do bloco, que vai ser a mesma do sistema como um todo!
Passo 2
Agora que já sabemos a aceleração do sistema como um todo, a gente consegue calcular a força usando a segunda lei do Nenê, também conhecido com Newton.
Como calculamos a força máxima de atrito, ela não pode passar disso ein!