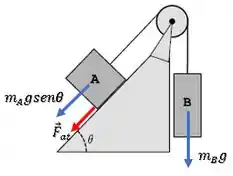
Dois blocos estão ligados por uma corda que passa por uma polia de massa desprezível e sem atrito em seu eixo, como mostra a figura ao lado.
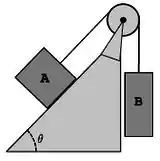
O bloco A tem massa e os coeficientes de atrito estático e cinético entre A e a rampa são respectivamente
e
Considere que os corpos são liberados a partir do repouso, , e .
(a) Determine a menor massa possível do bloco B acima da qual o bloco A sobe a rampa.
(b) Determine a maior massa possível do bloco B abaixo da qual o bloco A desce a rampa.
(c) Obtenha a aceleração do bloco A quando a massa de B é indicando o módulo, direção e sentido.
Passo 1
Nessa questão, a força peso tenta puxar os dois blocos para baixo, sendo que no bloco A, temos apenas a componente paralela à rampa exercendo esse papel.
Então, antes de considerar o atrito, dá uma olhada apenas nessas forças:
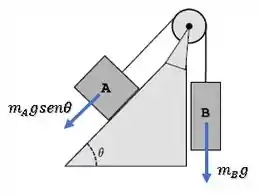
Esses bloquinhos estão em um “cabo de guerra”, cada um puxando para um lado.
Se o bloquinho B for muito pesado sua força peso vai vencer e puxar o bloquinho A para cima da rampa. Porém, se o bloquinho B for muito leve, a componente da força peso do bloquinho A vai vencer e puxar o bloquinho A para baixo da rampa. Nesse caso, só teríamos um valor para a massa que deixaria esse sistema em equilíbrio.
Mas aí que entra o atrito na jogada...

Agora, quando o bloco A tender a deslizar, vai aparecer uma força de atrito contra o movimento, mantendo o sistema em equilíbrio.
Se o bloco B for muito leve, o bloco A tende a deslizar para baixo:
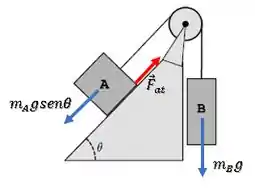
A aparece impedindo o bloco A de descer.
Já se o bloco B for muito pesado, o bloco A tende a deslizar para cima:
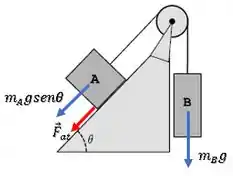
A aparece impedindo o bloco A de subir.
Então, como a força de atrito sempre vai estar sempre ajudando o bloco que está perdendo o “cabo de guerra”, não temos mais apenas um valor de que mantém o sistema em equilíbrio e sim um intervalo de .
Passo 2
(a) Determine a menor massa possível do bloco B acima da qual o bloco A sobe a rampa.
Para o bloco A subir a rampa, temos esse caso:
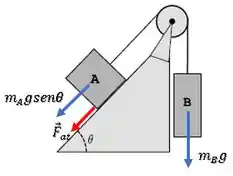
Então, nós queremos a menor que seja capaz de vencer a componente da força peso de A somada com a força de atrito estático máxima .
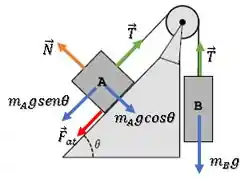
Para achar isso, vamos completar o nosso desenho, com as outras forças, lembrando que como a polia é ideal, a tração em todo o cabo é a mesma:
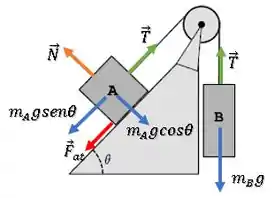
No bloco B, o somatório das forças na vertical é:
Já no bloco A, o somatório das forças paralelas à rampa é:
Logo, podemos juntar as duas equações, substituindo :
Lembrando que a força de atrito estática é dada pela expressão :
Agora, vamos achar essa força normal a partir do somatório em A das forças perpendiculares à rampa:
Então, ficamos com:
Podemos cortar em todos os termos e substituir os valores:
Assim, achamos que a partir de para o valor de , o bloco B consegue vencer o “cabo de guerra” e puxar o bloco A para cima.
Passo 3
(b) Determine a maior massa possível do bloco B abaixo da qual o bloco A desce a rampa.
Para o bloco A descer a rampa, temos esse caso:
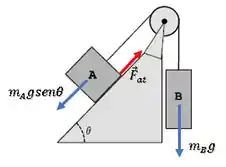
Então, nós queremos a maior que ainda permite a componente da força peso de A puxá-lo para baixo.
Vamos usar novamente o nosso diagrama de forças completo:
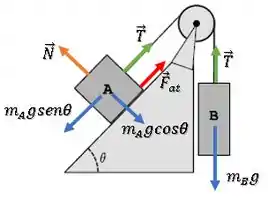
No bloco B, temos de novo que:
Já no bloco A, o somatório das forças paralelas à rampa será:
Juntando as duas:
A força de atrito estática máxima é :
E podemos achar a força Normal novamente com o somatório de forças em A na perpendicular à rampa:
Assim, ficamos com:
Cortando em todos os termos e arrumando a casa, temos:
Assim, achamos que até para o valor da massa de B , o bloco A vai conseguir vencer o “cabo de guerra” e descer pela rampa.
Passo 4
(c) Obtenha a aceleração do bloco A quando a massa de B é indicando o módulo, direção e sentido.
Resolvendo os itens (a) e (b), achamos que se estiver no intervalo entre e , o sistema estará em equilíbrio, pois a força normal é capaz de se opor às diferenças de peso entre os blocos.
Mas quando está fora desse intervalo, a força de atrito máxima é ultrapassada e os blocos entram em movimento. O atrito passa a ser cinético.
Para , temos que o bloco A será puxado por uma força que o faz subir a rampa. Logo, temos esse caso:
Então vamos fazer o somatório de forças e aplicar a segunda lei de Newton.
Usando nosso diagrama querido, temos em B que:
Se os blocos estão conectados, suas acelerações vão ser iguais. Então, para o bloco A, temos que:
Juntando as duas:
Agora que o atrito é cinético, vamos usar a expressão . Isolando a aceleração:
Como o bloco A está em equilíbrio na direção perpendicular à rampa, achamos que a força normal é:
Então, ficamos com:
Agora, basta substituir os valores que temos:
Achamos o módulo da aceleração. Sua direção será paralela à rampa e seu sentido para cima.
Resposta
(a)
(b)
(c) , paralela à rampa e para cima.